
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Плоскости симметрии
Плоскостью симметрии называется плоскость, которая делит фигуру на две равные части, расположенные друг относительно друга как предмет и его зеркальное отражение.
Плоскость симметрии обозначается буквой Р.
Симметрическое преобразование, отвечающее плоскости симметрии, есть отражение в плоскости.
| Рис. 2.2. Фигура несимметричная |

|
Для отражения некоторой фигуры АВD в плоскости Р (рис.2.3) из каждой её точки опускают перпендикуляры на плоскость отражения и продолжают их по другую сторону плоскости на расстояния, равные расстояниям отражаемых точек до плоскости Р. В результате получаем новую фигуру А1В1D1.

|
| Рис. 2.3. Отражение точек фигуры в плоскости Р |
При нахождении плоскостей симметрии мысленно рассекают их плоскостью на две половины так, чтобы при отражении в этой плоскости половинки совместились друг с другом.

|
Не каждая плоскость, делящая фигуру пополам, является плоскостью симметрии. Например, в прямоугольнике только две плоскости параллельные его сторонам являются плоскостями симметрии (рис. 2.4). Плоскости идущие вдоль диагоналей прямоугольника плоскостями симметрии не являются, т. к. образующиеся треугольники зеркально не равны.
| Рис.2.4. Прямоугольник АВDЕ имеет две плоскости (Р и Р1) симметрии |
Кристаллические многогранники могут иметь одну или несколько плоскостей симметрии. Число плоскостей симметрии указывается коэффициентом, стоящим перед буквой Р. Например, куб имеет 9Р, т. е. девять плоскостей симметрии (рис. 2.5).
Следует помнить, что плоскости симметрии или перпендикулярны к рёбрам и граням многогранника и проходят через их середины, или проходят вдоль рёбер.
Центр инверсии
Центром инверсии называется такая точка внутри фигуры, при отражении в которой всех точек последняя совмещается сама с собой.
Чтобы произвести отражение какой-либо точки фигуры в центре инверсии (рис. 2.6), нужно соединить эту точку и точку С прямой линией.
Как видно из рис. 2.6 плоскости треугольников параллельны, но стороны имеют противоположные
направления.
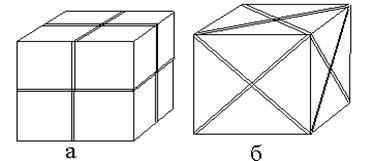
| Рис. 2.5. Куб имеет девять плоскостей симметрии (9Р): три главных плоскости (а) и шесть диагональных (б) |
Центр инверсии называют центром обратного равенства, потому что каждая грань при наличие центра инверсии должна иметь равную себе и обратно параллельную грань (рис. 2.7).
| Рис. 2.6. Треугольник АВD и А1В1D1, связанные центром инверсии, равны друг другу и обратно параллельны |


|
| Рис. 2.7. Многогранник с центром инверсии С: грани попарно равны и обратно параллельны |
| Рис. 2.8. Многогранник не имеет центра инверсии, т.к. для грани q нет парной параллельной грани |
Оси симметрии
Осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определённый угол фигура совмещается сама с собой.
Наименьший угол поворота, приводящий фигуру к самосовмещению, называется элементарным углом поворота оси. Элементарный угол поворота оси a содержится целое число раз в 360°:
360/a = n
где n – целое число.
Число n, показывающее сколько раз элементарный угол поворота оси содержится в 3600, называется порядком оси.
В геометрических фигурах могут присутствовать оси любых порядков, начиная от оси первого порядка и кончая осью бесконечного порядка.
Элементарный угол поворота оси первого порядка (n = 1) равен 3600. Так как каждая фигура, будучи повернута вокруг любого направления на 3600, совмещается сама с собой, то всякая фигура обладает бесконечным количеством осей первого порядка. Такие оси не являются характерными, поэтому они обычно не упоминаются.
Ось бесконечного порядка отвечает бесконечно малому элементарному углу поворота. Эта ось присутствует во всех фигурах вращения в качестве оси вращения.
Примерами осей третьего, четвертого, пятого, шестого и т. д. порядков являются перпендикуляры к плоскости рисунка, проходящие через центры правильных многоугольников, треугольников, квадратов, пятиугольников и т.п.
Таким образом, в геометрии существует бесконечный ряд осей различных порядков.
В кристаллических же многогранниках возможны не любые оси симметрии, а только оси первого, второго, третьего, четвертого и шестого порядка.
Оси симметрии пятого и выше шестого порядка в кристаллах невозможны. Это положение является одним из основных законов кристаллографии и называется законом симметрии кристаллов.
Как и др. геометрические законы кристаллографии, закон симметрии кристаллов объясняется решетчатым строением кристаллического вещества. Действительно, раз симметрия кристалла есть проявление симметрии его внутреннего строения, то в кристаллах возможны только такие элементы симметрии, которые не противоречат свойствам пространственной решетки.
Докажем, что ось пятого порядка не удовлетворяет законам пространственной решетки и тем самым докажем ее невозможность в кристаллических многогранниках.
Предположим, что ось пятого порядка в пространственной решетке возможна. Пусть эта ось будет перпендикулярна плоскости чертежа, пересекая ее в точке О (рис.2.9). В частном случае точка О может совпадать с одним из узлов решетки.

| Рис. 2.9. Ось симметрии пятого порядка невозможна в пространственных решетках |
Возьмем ближайший от оси узел решетки А1, лежащий в плоскости чертежа. Так как вокруг оси пятого порядка все повторяется пять раз, то ближайших к ней узлов в плоскости чертежа должно быть всего пять А1,А2,А3,А4,А5. Располагаясь на одинаковых расстояниях от точки О в вершинах правильного пятиугольника, они совмещаются друг с другом при повороте вокруг О на 360/5=72°.
Эти пять узлов, лежащие в одной плоскости, образуют плоскую сетку пространственной решетки и поэтому к ним приложимы все основные свойства решетки. Если узлы А1 и А2 принадлежат ряду плоской сетки с промежутком А1А2, то через любой узел решетки можно провести ряд, параллельный ряду А1А2. Проведем такой ряд через узел А3. Этот ряд, проходящий и через узел А5, должен иметь промежуток, равный А1А2, т. к. в пространственной решетке все параллельные ряды обладают одинаковой плотностью.
Следовательно, на расстоянии А3Аx = А1А2 от узла А3 должен находиться еще один узел Аx. Однако дополнительный узел Аx оказывается лежащим ближе к точке О, чем узел А1, взятый по условию ближайшим к оси пятого порядка.
Таким образом, сделанное нами допущение о возможности оси пятого порядка в пространственных решетках привело нас к явному абсурду и поэтому является ошибочным.
Поскольку существование оси пятого порядка несовместимо с основными свойствами пространственной решетки, то такая ось невозможна и в кристаллах.
Аналогичным образом доказывается невозможность существования в кристаллах осей симметрии выше шестого порядка и, наоборот, возможность в кристаллах осей второго, третьего, четвертого и шестого порядка, присутствие которых не противоречит свойствам пространственных решеток.
Для обозначения осей симметрии употребляется буква L, а порядок оси указывается маленькой цифрой, располагаемой справа от буквы (например, L4 - ось четвертого порядка).
В кристаллических многогранниках оси симметрии могут проходить через центры противоположных граней перпендикулярно к ним, через середины противоположных ребер перпендикулярно к ним (только L2) и через вершины многогранника. В последнем случае симметричные грани и ребра одинаково наклонены к данной оси.
Кристалл может иметь несколько осей симметрии одного порядка, количества которых указывается коэффициентом перед буквой. Например, в прямоугольном параллелепипеде присутствует 3L2, т. е. три оси симметрии второго порядка; в кубе имеются 3L4, 4L3 и 6L2, т. е. три оси симметрии четвертого порядка, четыре оси третьего порядка и шесть осей второго порядка и т. д.
Не нашли, что искали? Воспользуйтесь поиском: