
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Поверхности второго порядка в пространстве
Лабораторная работа 16. Построение графиков сложных функций средствами Microsoft Excel
Поверхности в трехмерном пространстве
В этом разделе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
Уравнение вида:
Ах+By+Cz+D=0
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D =0, то уравнение Ах+By+Cz= 0 определяет плоскость, проходящую через начало координат. Если А =0, то уравнение By+Cz+D =0 определяет плоскость, параллельную оси 0х; если А=D =0, то уравнение By+Cz =0 определяет плоскость, проходящую через ось 0т, если А=В =0, то уравнение Cz+D= 0 определяет плоскость, параллельную плоскости 0ху; если А=В = D =0, то уравнение Cz =0 (или z =0) определяет координатную плоскость 0ху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:

где а, b, с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку М(x1, y1, z1):
а(x–x1)+ (у–у1)+с(z – z1)= 0.
2. Уравнение плоскости, проходящей через три точки М1(x1, y1, z1), М2(х2, у2, z2), М3(х3, у3, z3):

В MS Excel Мастер диаграмм может быть также использован и для построения плоскостей. Необходимо ввести точки плоскости в рабочую таблицу, вызвать Мастер диаграмм, задать тип диаграммы, диапазоны данных и подписей оси х, ввести названия осей.
Упражнение 8.1. Рассмотрим построение плоскости в Excel на примере уравнения 2х+ 4y–2z+2=0. Пусть необходимо построить часть плоскости, лежащей в I квадранте (х Î[0; 6] с шагом D=0,5, у Î[0; 6] с шагом D=1).
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере z=х+2у+ 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение: = $А2+2*В$1+1, предварительно переключившись на английский язык (Alt+Shift). Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной х и строки 1 — переменной у. Затем автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица:

На панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных В2:Н14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого следует активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и ввести диапазон подписей оси х — А2:А14.
Далее вводим значения подписей оси у. Для этого в рабочем поле Ряд указываем первую запись Ряд 1 и в рабочее поле Имя, активировав его указателем мыши, вводим первое значение переменной у: 0. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: 1. Повторяем таким образом до последней записи — Ряд 7. В результате вкладка Ряд будет иметь следующий вид.

После появления требуемых записей необходимо нажать кнопку Далее.
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы, ввести с клавиатуры в данное поле название: Плоскость. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.
Далее нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграмма.

Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах2+By2+Cz2+2Dxy+2Eyz+2Fzx + 2Gx+2Hy+2Kz+L=0. (7.6)
Причем коэффициенты А, В, С, D Е, F не могут быть равны нулю одновременно.
Частными случаями уравнения (7.6) являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
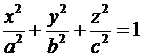 (7.7)
(7.7)
Это уравнение называется каноническим уравнением эллипсоида.
Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии.
Для построения эллипсоида в Excel каноническое уравнение (7.7) необходимо разрешить относительно переменной z (представить в виде z=f(x, у)).
Упражнение 8.2. Рассмотрим построение эллипсоида в Excel на примере уравнения:

Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î[–3; 3], у Î[–2; 2] с шагом D=0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере

Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (–2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (–1,5). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
Далее вводим значения переменной z. Для этого табличный курсор необходимо поместить в ячейку В2 и на панели инструментов Стандартная нажать кнопку Вставка > Функции… (fx). В появившемся диалоговом окне Мастер функций- шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция выбираем функцию Корень. Нажимаем кнопку ОК. Появляется диалоговое окно Корень. В рабочее поле вводим подкоренное выражение: 1 — $А2^2/9-В$1^2/4. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной х истроки 1 — переменной у. Нажимаем кнопку ОК. В ячейке В2 появляется #ЧИСЛО!
(при х=–3 и у=–2 точек рассматриваемого эллипсоида не существует).
Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) — в диапазон ВЗ:J14.
В результате должна быть получена следующая таблица точек эллипсоида.

Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных B2:J14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого щелкните в нем указателем мыши и введите диапазон подписей оси х — А2: A14.
Вводим значения подписей оси у. Для этого в рабочем поле Ряд указываем первую запись Ряд 1 и в рабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи — Ряд 9.
После появления требуемых записей необходимо нажать кнопку Далее.
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Эллипсоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.
Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграммаэллипсоида.

Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
 . (7.8)
. (7.8)
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
 . (7.9)
. (7.9)
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши.
Уравнения (7.8) и (7.9) называются каноническими уравнениями гиперболоидов.
Для построения гиперболоида в Excel канонические уравнения (7.8) или (7.9), как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z=f(х, у)).
Упражнение 8.3. Рассмотрим построение двухполостного гиперболоида вида
 .
.
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: х Î[–3; 3], у Î[–2; 2] с шагом D=0,5 для обеих переменных.
Выполнение. Вначале необходимо разрешить уравнение относительно переменной г. В примере

Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ x. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3). В ячейку A3 — второе значение аргумента — левая граница диапазона плюс шаг построения (–2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 — второе значение переменной — левая граница диапазона плюс шаг построения (–1,5). Затем, выделив блок ячеек В1:С1,автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
Далее вводим значения переменной z. Для этого табличный курсор необходимо поместить в ячейку В2 и на панели инструментов Стандартная нажать кнопку Вставка > Функции… (fx). В появившемся диалоговом окне Мастер функций - шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция выбираем функцию Корень. Нажимаем кнопку ОК. Появляется диалоговое окно Корень. В рабочее поле вводим подкоренное выражение: 1 + $А2^2/9 + В$1^2/4. Нажимаем кнопку ОК. В ячейке В2 появляется 1,732051. Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) — в диапазон ВЗ:J14.
В результате должна быть получена следующая таблица точек гиперболоида.

Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных В2:J14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого следует активизировать данное поле, щелкнув в нем указателем мыши, и ввести в него диапазон подписей оси х — А2:А14.
Вводим значения подписей оси у. Для этого в рабочем поле Ряд выбираем первую запись Ряд 1 и в рабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд выбираем вторую запись — Ряд 2 и в рабочее поле Имя вводим второе значение переменной у:
–1,5. Повторяем таким образом до последней записи — Ряд 9.
После появления требуемых записей необходимо нажать кнопку Далее.
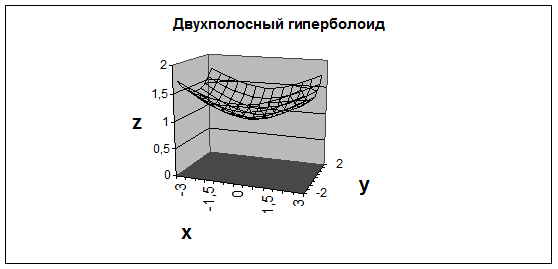
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Далее щелкнув в рабочем поле Название диаграммы, ввести в него с клавиатуры название: Двухполостный гиперболоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.
Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграмма двухполостного гиперболоида.
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
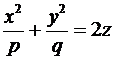
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением

Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Упражнение 8.4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: x Î[–3; 3], у Î[–2; 2] с шагом D=0,5 для обеих переменных.
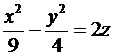 .
.
Выполнение. Вначале необходимо разрешить уравнение относительно переменной z. В примере

Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3). В ячейку A3 — второе значение аргумента — левая граница диапазона плюс шаг построения (–2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 — второе значение переменной — левая граница диапазона плюс шаг построения (– 1,5). Затем, выделив блок ячеек В1:С1,автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
Далее вводим значения переменной z. Для этого табличный курсор необходимо поместить в ячейку В2 и ввести формулу — = $А2^2/18 -В$1^2/8, после чего нажать клавишу Enter. В ячейке В2 появляется 0. Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) — в диапазон В2:J14.
В результате в диапазоне В2:J14 появится таблица точек гиперболического параболоида.
Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных В2:J14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого следует активизировать данное поле, щелкнув в нем указателем мыши, и ввести диапазон подписей оси х — А2:А14.
Вводим значения подписей оси у. Для этого в рабочем поле Ряд выбираем первую запись Ряд 1 и, активизировав рабочее поле Имя указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд выбираем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи — Ряд 9.
После появления требуемых записей следует нажать кнопку Далее.
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого нужно выбрать вкладку Заголовки, щелкнув на ней указателем мыши. После чего в рабочее поле Название диаграммы ввести с клавиатуры название: Гиперболический параболоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.
Далее нужно нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграмма гиперболического параболоида.

Не нашли, что искали? Воспользуйтесь поиском: