Конус второго порядка

Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

.

Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.

В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.

ЗАДАНИЯ 8.1

25.Построить плоскость, параллельную плоскости 0ху и пересекающую ось 0z в точке М (0, 0, 2). Диапазоны изменения переменных х и у: х Î[0; 6] с шагом D=0,5, у Î[0; 6] с шагом D=1.

26.Построить плоскость, отсекающую на координатных осях отрезки а=3, b=2 и с =1. Диапазоны изменения переменных х и у: х Î[–1; 4] с шагом D=0,5, уÎ[–1; 3] с шагом D=1.

27.Построить плоскость, проходящую через точки М ₁(3, 3, 1), М ₂(2, 3, 2), М ₃(1, 1, 3). Диапазоны изменения переменных х и у: х Î[–1; 4] с шагом D=0,5, у Î[–1; 3] с шагом D=1.

28.Построить верхнюю часть эллипсоида:

.

Диапазоны изменения переменных х и у: х Î[–2; 2] с шагом D=0,5, у Î[–3; 3] с шагом D=1.

29.Построить верхнюю часть однополостного гиперболоида:

Диапазоны изменения переменных х и у: х Î[–3; 3] с шагом D =0,5, у Î[–4; 4] с шагом D=1.

30.Построить эллиптический параболоид:

.

Диапазоны изменения переменных х и у: х Î[–2; 2] с шагом D=0,5, у Î[–3; 3] с шагом D=1.

31.Построить верхнюю часть конуса

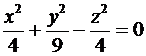
Диапазоны изменения переменных х и у: х Î[–2; 2] с шагом D=0,5, у Î[–3; 3] с шагом D=1.

Предъявите работу преподавателю

Не нашли, что искали? Воспользуйтесь поиском: