Естественно-научное обоснование сходящейся (нелинейной) спирали развития. Проблема формального описания процессов самоорганизации, обоснования количественных критериев уровня организации

Проблема формального описания процессов самоорганизации, обоснования количественных критериев уровня организации, обладающих большой общностью, и, главное, проблема создания мысленной модели процессов самоорганизации, синтезирующей диалектические законы с современными естественно-научными представлениями о процессах развития, приобретают особое значение. При этом количественный информационный критерий является достаточно универсальным и адекватно описывает процессы, которые в нашей философской литературе излагаются как процессы перехода от простого к сложному, от менее организованного к более организованному.

Как мысленная модель процесса самоорганизации, сходящаяся спираль более адекватна современным представлениям о процесс саморазвития, ибо она:

• показывает, что формирование новой структуры начиняется не с непонятной "невидимой точки", а с максимальной (реально существующей) энтропии (хаоса, неопределенности);
• строится в координатах информации-энтропии и отображает возрастание уровня организации объекта во времени;
• объясняет ограниченность числа витков спирали этапом переходного процесса, носящего явно выраженный спиралевидные характер;
• как отображение процесса самоорганизации, сходящаяся спираль имеет определенное сходство с колебательным процессом в устойчивых системах авторегулирования. "Гомеостат, - писал У. Эшби, - в некотором смысле не делает ничего кроме того, что движется к состоянию равновесия" [13]. С этим фундаментальным положением как нельзя лучше согласуется именно сходящаяся форма спирали. Речь у Эшби идет о равновесии смысле негэнтропийной устойчивости неравновесной системы, отдалившейся от уровня максимальной энтропии ("равновесия");
• отображает нелинейность процессов самоорганизации.

В конце процесса самоорганизации, когда "архитектура" объекта в основном определилась и наступает насыщение информацией, сходящаяся спираль постепенно "выпрямляется", отображая переход объекта в эволюционную стадию развития.

Каждый этап развития в реальных процессах имеет свою внутреннюю диалектику. Например, экономическим формациям характерны восходящие и нисходящие линии развития. Пока производственные отношения данной формации более или менее соответствуют уровню производительных сил, последние развиваются ускоренно, по восходящей линии. А когда устоявшиеся производственные отношения начинают тормозить продолжающийся рост производительных сил, тогда наступает застойная или даже нисходящая стадия в развитии этой формации, что в итоге подводит общество к революционной ситуации, к новому скачку в развитии.

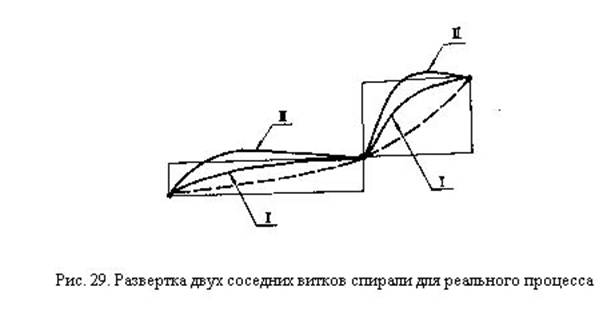
На рис. 29 дана развертка двух соседних витков спирали (пунктирная линия - идеализированный процесс). Динамика реальных процессов изображена кривыми I и II, причем на кривой II восходящие и нисходящие стадии более резко выражены. При переносе этого построения витки спирали будут иметь вид, изображенный на рис. 28 множеством точек (на одном из витков).

Не нашли, что искали? Воспользуйтесь поиском: