Основні закони логічного мислення

Закон тотожності є одним із законів правильного мис­лення, дотримання якого гарантує визначеність та ясність мислення. Закон формулюється так: «У процесі певного мірку­вання всяке поняття і судження повинні бути тотожніми самі собі» (а = а). Тотожність є рівність, подібність предметів у пев­ному відношенні.

У процесі мислення закон тотожності виступає як норма­тивне правило (принцип). Він означає, що в процесі міркуван­ня не можна підміняти одну думку іншою, одне поняття дру­гим. Не можна тотожні думки видавати за різні, а різні - за тотожні. Наприклад, тотожніми за об'ємом будуть такі три поняття: вчений, з ініціативи якого було засіювано Московсь­кий університет; вчений, що сформулював закон збереження матерії та руху; вчений, що у 1745 році став першим російсь­ким академіком Петербурзької Академії наук, - оскільки вони будуть позначати одну і ту ж людину (М.В. Ломоносова), але дають різну інформацію про неї.

Порушення закону тотожності призводить до двознач­ності. Наприклад, «Ноздрьов був у певному відношенні істо­ричною людиною, на жодних зборах, де він був, не обходилось без історії» (М.Гоголь). Гра слів тут побудована на викорис­танні омонімів.

Порушення закону тотожності виявляється і тоді, коли люди­на виступає не по тій темі, що обговорюється, свавільно підміняє один предмет обговорення іншим, використовує терміни і понят­тя не в тому розумінні, в якому це прийнято, не попереджає про це. Наприклад, ідеалістом іноді вважають людину, що вірить в іде­али, живе заради високої мети; у філософії ж ідеаліст - це мисли­тель, який вважає, що ідеальне породжує матеріальне. Іноді в ході дискусій суперечка по суті підміняється суперечкою про слова: люди говорять про різні речі, думаючи, що мають на увазі одну і ту саму людину, подію. Логічні помітки часто роблять при вико­ристанні омонімів, тобто слів, що мають два значення («матерія», «зміст» тощо). Наприклад: «Учні прослухали пояснення вчителя». В результаті ототожнення різних понять виникає логічна помил­ка, що називається «підміною понять».

Коли ж в ході обгрунтування або спростування висунута теза осмислено або неусвідомлено підміняється іншою, то ви­никає друга помилка - «підміна тези». Щоб відволікти увагу від головного, намагаються наговорити багато непотрібного, підмінити одне питання іншим, приписати опоненту те, чого він не говорив.

Сутність закону непротиріччя полягає в тому, що «два про­тилежні судження не можуть бути істинними а один і той самий час, і в одному і тому самому відношенні». Формула його виглядає так: а ^ а). Наприклад, «Фейєрбах - автор «Сутності християн­ства» та «Фейєрбах не є автором «Сутності християнства».

Якщо в мисленні людини виявлено формально-логічне про­тиріччя, то таке мислення вважається хибним, а судження, з якого витікає протиріччя, заперечується або вважається хибою. Тому в полеміці при спростуванні думки опонента широко використовується метод «приведення до абсурду».

Закон виключеного третього формулюється так: «З двох суперечливих суджень одне істинне, друге - хибне, а третього не може бути». Суперечливими (контрадикторними) назива­ються такі два судження, в одному з яких щось стверджується про предмет, а в іншому те саме про цей предмет заперечуєть­ся; тому вони не можуть бути обидва істинними або хибними. Одне з них - істина, а друге обов'язково - хиба. Такі суджен­ня називаються заперечуючими одне одного. Наприклад, «Всі гриби їстивні» та «Жоден гриб не є їстивним». Цей закон не може бути застосований там, де відображується невизначеність в об'єктивних процесах або в самому процесі пізнання; тоді можливий третій варіант. Наприклад, тоді людина може голо­сувати: «за», «проти», «утримався».

Закон достатніх засад формулюється так: «Будь-яка істинна думка повинна бути достатньо обгрунтованою». Мова іде про обгрунтування саме і тільки істинних думок, бо хибу довести неможливо. Як аргументи для підтвердження істинної думки можуть бути використані істинні судження, цифровий матеріал, статистичні дані, закони науки, аксіоми, теореми тощо.

Логічна основа і логічний наслідок не завжди співпадають з реальними причинами і наслідком. Так, наприклад, дощ є ре­альною причиною того, що дахи домів мокрі. Логічна основа і наслідок будуть якраз зворотніми, оскільки, визирнувшії у вікно і побачивши мокрі дахи будинків (логічна основа), ми вважаємо, що «Йшов дощ».

Висновок

Формами мислення є поняття, судження і умовиводи. Опо­середковано, завдяки різним видам умовиводів, ми можемо отримувати нові знання. Побудувати умовивід можна при на­явності одного або кількох істинних суджень (посилань), що поставлені у взаємозв'язок. Висновок - це форма мислення, в якій з одного або кількох суджень на основі певних правил вис­новку можна отримати нове судження, що з необхідністю або певним ступенем імовірності випливає з них. Виведення наслідків з даних посилань - широко розповсюджена логічна операція. Умовами істинності висновку є істинність посилань та логічна слушність виводу.

Висновки поділяються на дедуктивні, індуктивні та виснов­ки за аналогією.

Дедуктивні висновки - це ті висновки, у котрих між поси­ланнями та. висновком є відношення логічного руху. Наприклад,

Всі риби дихають зябрами.

Всі окуні - риби.

Всі окуні дихають зябрами.

Тут перше посилання «Всі риби дихають зябрами» є загальностверджувальним судженням і виражає більший ступінь уза­гальнення порівняно з висновком, що також є загальностверджувальним судженням «Всі окуні дихають зябрами». Ми будуємо висновок від ознаки, що притаманна роду («риба»), до її приналежностідо виду - «окунь», тобто від загального класу до його конкретного випадку, підкласу.

Категоричний силогізм - це вид дедуктивного висновку, у якому з двох істинних категоричних суджень, де S і Р пов'я­зані середнім терміном, при виконанні правил з необхідністю слідує висновок.

Всі метали (М) проводять струм (Р) - більше посилання.

Мідь (S) є метал (М) - менша посилка.

Мідь (S) проводить електричний струм (Р) - висновок.

Поняття, що входять до складу силогізму, називаються термінами силогізму. У наведеному прикладі термінами є: Р («електропровідник) - більший термін, це предикат виснов­ку; 5 («мідь») - менший термін, це суб'єкт висновку; М («ме­тал») - середній термін, що служить для зв'язування S і Р і відсутній у висновку.

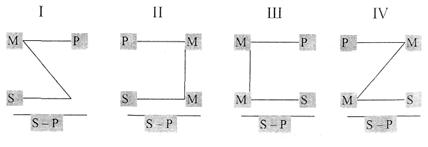Фігурами категоричного силогізму називаються форми, що розрізняються за положенням середнього терміну М у посилан­нях. Розрізняються чотири фігури.

Приклади.

1.Всі квіти (М) - рослини (Р). Троянда (S) - квітка (М). Троянда (S) - рослина.

2. Всі вужі (Р) - плазуни (М).

Ця тварина (S) не є плазуном (М). Ця тварина (S) не є вужем(Р).

3. Всі вуглеці (М) - прості тіла (Р). Всі вуглеці (М) - електропровідні ( S).

Деякі електропровідники (S) - прості тіла (Р).

4. Всі кити (Р) - ссавці (М). Жоден ссавець (М) не є рибою (S). Жодна риба (S) не с китом (Р).

Загальні правила фігур:

I фігура Більше посилання має бути загальною, менша - стверджувальною.

II фігура Більше посилання загальне і одне з посилань, а також висновок заперечувальні.

ІІІ фігура Менше посилання має бути стверджувальним, а висновок - окремим.

IV фігура Загальностверджувальних висновків не дає.

Дедуктивні висновки дозволяють виводити з істинних по­силань при дотриманні відповідних правил істинні висновки. Індуктивні висновки звичайно дають нам не достовірні, а лише правдоподібні заключення. Повною індукцією називається та­кий висновок, у якому загальний висновок про всі елементи класу предметів робиться на основі розгляду кожного елемента цього класу. Щоб використовувати повну індукцію, потрібно: по пер­ше, точно знати число предметів та явищ, що належить розгля­нути, по-друге, впевнитись, що ознака притаманна кожному елементу цього класу.

Неповна індукція застосовується у тих випадках, коли: по-перше, неможливо розглянути всі елементи класу явищ, що нас Цікавить; по-друге, якщо число об'єктів нескінченне, або скінченне, але досить велике; по-третє, розгляд знищує об'єкт (наприклад,«Всі дерева мають корені»). Тоді розглядаються не всі предмети та явища, а висновок робиться про всі.

В залежності від способів обгрунтування висновку непов­на індукція поділяється на три види:

1. Індукція через просте перелічування, перерахування (популярна індукція), коли на основі повторення ознак у низки однорідних предметів робиться загальний висновок про притаманність цієї ознаки всім предметам та явищам. На основі популярної індукції довгий час вважали, що всі лебеді білі, поки в Австралії не зустріли чорних. Народні прикмети (ластівки низько літають - бути дощу, червоний захід сонця – завтра буде вітер) виведені на основі популярної індукції.

2. Індукція через аналіз та відбір фактів, коли вивчаються планомірно відібрані, найбільш типові предмети, Так обчислюють середню урожайність поля, судять про якість великих партій товару, перевіряють схожість насіння тощо. При цьому проводять різні види виборки: стихійну, квотну, вірогідну та інші.

3. Наукова індукція - висновок, у якому на основі пізнання необхідних ознак або необхідного зв'язку частини предметів класу робиться загальний висновок про всі предмети цього класу. Така індукція дає достовірний висновок.

Аналогія - це висновок про притаманність предмету певної ознаки (тобто властивості або відношення) на основі подібності в ознаках з пішим предметом. У формі такого висновок здійснюється приписування предмета властивості або перене­сення відносин. Завдяки аналогії здійснюється перенос інфор­мації з одного предмета (моделі) на інший (прототип). Поси­лання належать до моделі, висновок - до прототипу.

Залежно від характеру інформації, що переноситься з моделі на прототип, аналогія поділяється на два види: аналогія власти­востей і аналогія відносин. Залежно від ступеня достовірності висновки за аналогією можна поділити на три види: 1) сувора аналогія, що дає достовірний висновок; 2) несувора аналогія, щ о дає вірогідний висновок; 3) хибна (вульгарна) аналогія, що дає неправдивий, хибний висновок.

Не нашли, что искали? Воспользуйтесь поиском: