Лабораторная работа №4. Электрическая мощность

Электрическая мощность

Цель работы: измерить мощность, рассеиваемую резистором; определить КПД линии электропередач; исследовать согласование источника напряжения и нагрузки.

Задачи:

1. Выполнить эксперименты по исследованию электрических цепей, содержащих резисторы.

2. Построить графики.

3. Сделать выводы по работе.

Общие сведения.

Законы Кирхгофа.

Все электрические цепи подчиняются первому и второму законам (правилам) Кирхгофа. Первый закон Кирхгофа можно сформулировать двояко:

1. алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;

2. сумма подтекающих к любому узлу токов равна сумме утека­ющих от узла токов.

Применительно к рис. 4.1, если подтекающие к узлу токи счи­тать положительными, а утекающие – отрицательными, то соглас­но первой формулировке

согласно второй

Физически первый закон Кирхгофа означает, что движение за­рядов в цепи происходит так, что ни в одном из узлов они не скапли­ваются. Второй закон Кирхгофа также можно сформулиро­вать двояко:

1. алгебраическая сумма падений напряжения в любом замкну­том контуре равна алгебраической сумме ЭДС вдоль того же кон­тура:

(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);

2. алгебраическая сумма напряжений (не падений напряже­ния!) вдоль любого замкнутого контура равна нулю:

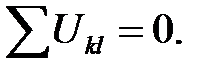
Для периферийного контура схемы рис. 4.1

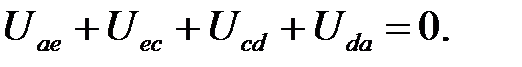
Законы Кирхгофа справедливы для линейных и нелинейных це­пей при любом характере изменения во времени токов и напряже­ний.

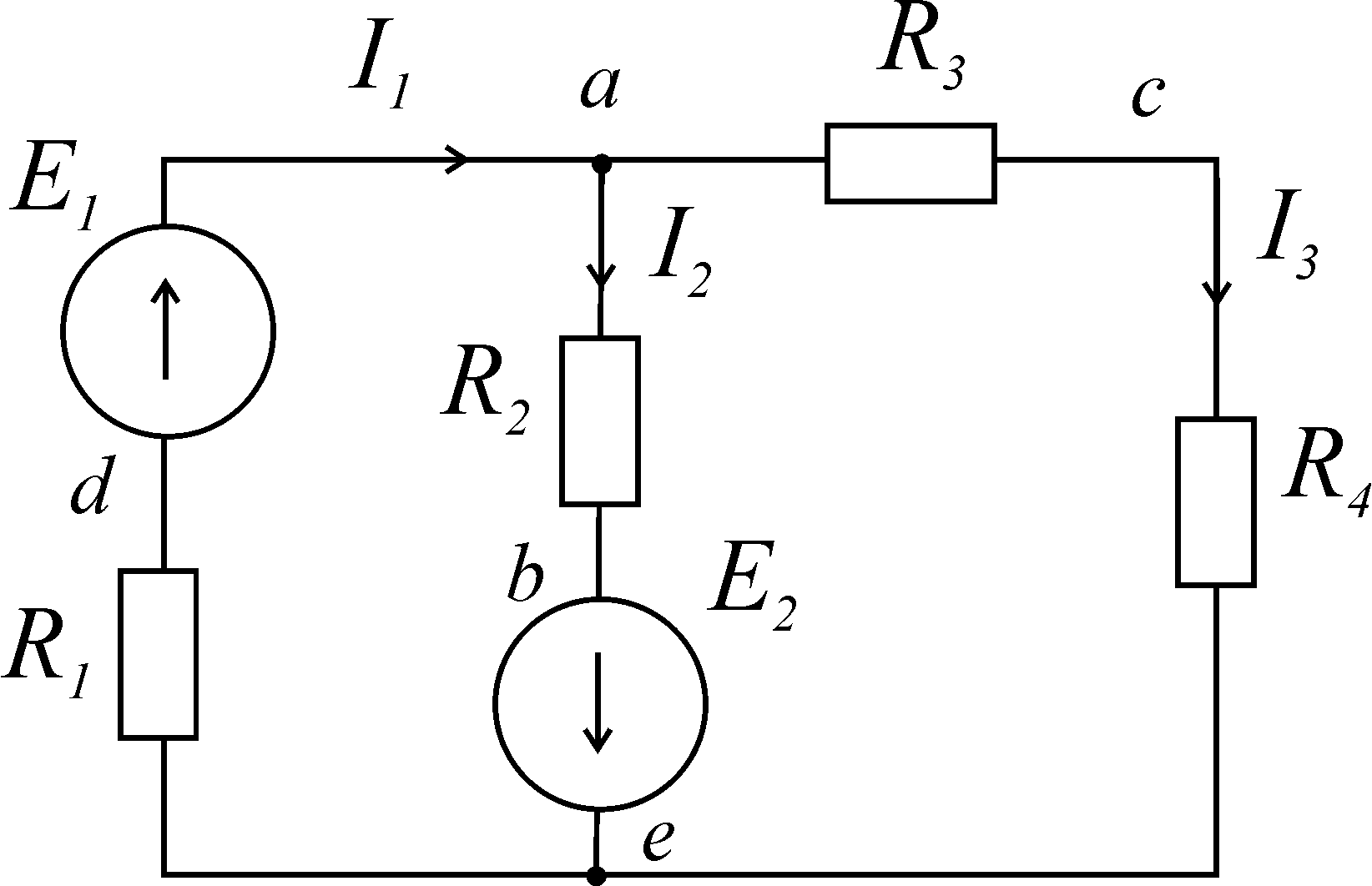
Рис. 4.1

Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы в, число ветвей, содержащих источники тока, – в _ит и число узлов у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется в–в _ит. Перед тем как составить уравнения, необходимо произ­вольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

С целью единообразия рекомендуется для всех контуров поло­жительные направления обхода выбирать одинаковыми, например по часовой стрелке. Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют уравнения, число которых равно чис­лу узлов без единицы, т. е. у– 1.

Уравнение для последнего y -го узла не составляют, так как оно совпало бы с уравнением, полученным при суммировании уже со­ставленных уравнений для у– 1 узлов, поскольку в эту сумму входили бы дважды и с противоположными знаками токи ветвей, не подходящих к у- му узлу, а токи ветвей, подходящих к у- му узлу, входили бы в эту сумму со знаками, противоположными тем, с какими они вошли бы в уравнение для у- го узла.

По второму закону Кирхгофа составляют уравнения, число ко­торых равно числу ветвей без источников тока (в–в _ит), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е. (в–в _ит)– (у– 1) = в–в _ит– у+ 1.

Составляя уравнения по второму закону Кирхгофа, следует ох­ватить все ветви схемы, исключая лишь ветви с источниками тока. Такие ветви как правило заменяют эквивалентной схемой, содержащей источник напряжения.

При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошед­шая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся называть независимыми.

Требование, чтобы в каждый новый контур входила хотя бы одна новая ветвь, является достаточным, но не необходимым условием, а потому его не всегда выполняют. В таких случаях часть уравнений по второму закону Кирхгофа составляют для контуров, все ветви которых уже вошли в предыдущие контуры.

Не нашли, что искали? Воспользуйтесь поиском: