Числа с плавающей точкой.

Для представления чисел с плавающей точкой используется полулогарифмическая форма записи числа:

N = ± m q^±p

где q – основание системы счисления,

±p – порядок числа,

m – мантисса числа .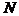

Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо.

Пример:

3,1415₍₁₀₎ = 314,15 × 10^-2 = 31415 × 10^-4 = 0,00031415 × 10⁴ = …

Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: . Таким образом, в нормализованных числах цифра после точки должна быть значащей.

Пример:

314,15 × 10^-2 = 0,31415 × 10¹

Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка.

а) представление чисел в формате полуслова:

Знак p

б) представление чисел в формате слова:

Знак p

…

Наиболее типично представление чисел с плавающей точкой в формате машинного слова (32 разряда).

Пример:

а) Число А = 4₍₁₀₎ = 100₍₂₎ = 0,1 × 10¹¹ (здесь 10₍₂₎ = 2₍₁₀₎ и 11₍₂₎ = 3₍₁₀₎ – переместили запятую на 3 двоичных порядка) записывается в ячейку следующим образом:

			Порядок p (7 разрядов)		Мантисса m (23 разряда)

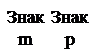б) Число А = – 0,01953125₍₁₀₎ = – 0,00000101₍₂₎ = – 0,101 × 10^–101:

			Порядок p (7 разрядов)		Мантисса m (23 разряда)

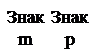Максимальным числом, представимым в формате машинного слова будет А @ (1 × 2¹²⁷)₍₁₀₎:

			Порядок (p = 127(10))
			Мантисса (m = 0,11111111111111111111111)(2)

Минимальным числом, представимым в формате машинного слова будет А @ (– 1 × 2¹²⁷)₍₁₀₎:

			Порядок (p = 127(10))
			Мантисса (m = 0,11111111111111111111111)(2)

Минимальным по модулю, отличным от нуля и нормализованным будет А = :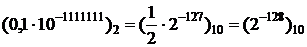

			Порядок (p = 127(10))
			Мантисса (m = 0,10000000000000000000000)(2)

Таким образом числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от – 1 × 2¹²⁷ до 1 × 2¹²⁷ (2¹²⁷» 10³⁸), а точность определяться мантиссой, состоящей из 23 разрядов. То есть можно различить два значения, разность между которыми составляет 2^–23» 10^–7.

Для иллюстрации приведенных значений отметим, что масса электрона» 10^–30 кг, масса Земли» 5,976 × 10²⁴ кг, масса Солнца» 2 × 10³⁰ кг.

Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью, т. е. число записывается в двух подряд ячейках памяти.

			Порядок p (7 разрядов)		Мантисса m (55 разрядов)

Двоичная арифметика

Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.

Таблица двоичного сложения	Таблица двоичного вычитания	Таблица двоичного умножения
0+0=0 0+1=1 1+0=1 1+1=10	0-0=0 1-0=1 1-1=0 10-1=1	0 0=0 0 1=0 1 0=0 1 1=1

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.

Пример. Выполнить сложение двоичных чисел:
а) X=1101, Y=101;

Результат 1101+101=10010.

б) X=1101, Y=101, Z=111;

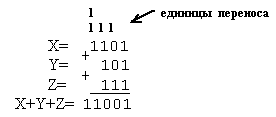
Результат 1101+101+111=11001.

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.

Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.

Результат 10010 - 101=1101.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример. 1001 101=?

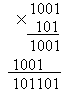
Результат 1001 101=101101.

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример. 1100.011: 10.01=

Результат 1100.011: 10.01=101.1.

Не нашли, что искали? Воспользуйтесь поиском: