
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Критерий различимости Фано
При реализации неравномерных кодов возникает проблема различимости кодов разных знаков. Для равномерных кодов она значительно менее значима ввиду точно известного количества элементарных сигналов в каждой кодовой комбинации – цепочек равной длины, не требующих разделителя.
Проблема различимости неравномерных кодов может быть решена формированием специального сигнала разделителя знаков кода, но это уменьшает эффективность передачи информации в целом. Другой подход к решению этой проблемы состоит в использовании критерия различимости Фано: в кодовом словаре никакой из кодов не должен совпадать с началом (префиксом) какого либо более длинного кода
Например, если имеется код 110, то в кодовом словаре не должно быть кодов 1, 11, 1101, 110101 и подобных. Тривиальное удовлетворение условию Фано – каждое кодовое слово начинать специальным знаком-разделителем. Можно придумать код и без разделителя.
Код Шеннона – Фано
Оптимальным кодом можно определить тот, в котором каждый двоичный символ будет передавать максимальную информацию. В силу формул Хартли и Шеннона максимум энтропии достигается при равновероятных событиях, следовательно, двоичный код будет оптимальным, если в закодированном сообщении символы 0 и 1 будут встречаться одинаково часто.
Рассмотрим в качестве примера оптимальное двоичное кодирование букв русского алфавита вместе с символом пробела «-». Полагаем, что известны вероятности появления в сообщении символов русского алфавита, например, приведенные в таблице 1
Табл. 1
Частота букв русского языка (предположение)
| Буква | Частота | Буква | Частота | Буква | Частота | Буква | Частота |
| «» | 0,145 | р | 0,041 | я | 0,019 | х | 0,009 |
| о | 0,095 | в | 0,039 | ы | 0,016 | ж | 0,008 |
| е | 0,074 | л | 0,036 | з | 0,015 | ю | 0,007 |
| а | 0,064 | к | 0,029 | ъ, ь | 0,015 | ш | 0,006 |
| и | 0,064 | м | 0,026 | б | 0,015 | ц | 0,004 |
| т | 0,056 | д | 0,026 | г | 0,014 | щ | 0,003 |
| н | 0,056 | п | 0,024 | ч | 0,013 | э | 0,003 |
| с | 0,047 | у | 0,021 | й | 0,010 | ф | 0,002 |
К. Шеннон и Р. Фано независимо предложили в 1948-1949 гг. способ построения кода, основанный на выполнении условия равной вероятности символов 0 и 1 в закодированном сообщении.
Все кодируемые символы (буквы) разделяются на две группы так, что сумма вероятностей символов в первой группе равна сумме вероятностей символов второй группы (то есть вероятность того, что в сообщении встретится символ из первой группы, равна вероятности того, что в сообщении встретится символ из второй группы). Для символов первой группы значение первого разряда кода присваивается равным «0», для символов второй группы – равными «1». Далее каждая группа разделяется на две подгруппы, так чтобы суммы вероятностей знаков в каждой подгруппе были равны. Для символов первой подгруппы каждой группы значение второго разряда кода присваивается равным «0», для символов второй подгруппы каждой группы – «1». Такой процесс разбиения символов на группы и кодирования продолжается до тех пор, пока в подгруппах не остается по одному символу. Пример кодирования символов русского алфавита приведен в табл.2.
Табл. 2.
Пример кодирования букв русского алфавита с помощью кода Шеннна-Фано.
| Буквы | Частоты | Двоичные разряды | ||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | ||
| «» | 0,145 | |||||||||
| о | 0,095 | |||||||||
| е | 0,074 | |||||||||
| а | 0,064 | |||||||||
| и | 0,064 | |||||||||
| т | 0,056 | |||||||||
| н | 0,056 | |||||||||
| с | 0,047 | |||||||||
| р | 0,041 | |||||||||
| в | 0,039 | |||||||||
| л | 0,036 | |||||||||
| к | 0,029 | |||||||||
| м | 0,026 | |||||||||
| д | 0,026 | |||||||||
| п | 0,024 | |||||||||
| у | 0,021 | |||||||||
| я | 0,019 | |||||||||
| ы | 0,016 | |||||||||
| з | 0,015 | |||||||||
| ъ, ь | 0,015 | |||||||||
| б | 0,015 | |||||||||
| г | 0,014 | |||||||||
| ч | 0,013 | |||||||||
| й | 0,010 | |||||||||
| х | 0,009 | |||||||||
| ж | 0,008 | |||||||||
| ю | 0,007 | |||||||||
| ш | 0,006 | |||||||||
| ц | 0,004 | |||||||||
| щ | 0,003 | |||||||||
| э | 0,003 | |||||||||
| ф | 0,002 |
Анализ приведенных в таблице кодов приводит к выводу, что часто встречающиеся символы кодируются более короткими двоичными последовательностями, а редко встречающиеся - более длинными. Значит, в среднем для кодирования сообщения определенной длины потребуется меньшее число двоичных символов 0 и 1, чем при любом другом способе кодирования.
Вместе с тем процедура построения кода Шеннона-Фано удовлетворяет критерию различимости Фано. Код является префиксным и не требует специального символа, отделяющего буквы друг от друга для однозначного декодирования двоичного сообщения.
При построении кода Шеннона-Фано для произвольного алфавита теоретический предел максимального значения информации в расчете на один двоичный символ составляет 1 бит. Для оценки степени близости составленного кода к оптимальному вычислим среднее количество информации, содержащейся в одной букве кодируемого алфавита, то есть энтропию Н в расчете на одну букву:
H = - 
где р  (j =0,1,...,31) – вероятность того, что символ примет определенное значение (от пробела до буквы Ф). Подставляя в формулу соответствующие значения вероятностей появления символов упрощенного русского алфавита из таблицы 1, и проводя вычисления, получим Н
(j =0,1,...,31) – вероятность того, что символ примет определенное значение (от пробела до буквы Ф). Подставляя в формулу соответствующие значения вероятностей появления символов упрощенного русского алфавита из таблицы 1, и проводя вычисления, получим Н 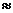 4,42 бита на один символ текста.
4,42 бита на один символ текста.
Вычислим среднее число двоичных символов mcp в расчете на одну букву в коде Шеннона-Фано:
mcp = 
где р  - частота появления j -го символа (берется из табл. 1), а m
- частота появления j -го символа (берется из табл. 1), а m  - число двоичных символов в коде Шеннона-Фэно данного j -го символа (считается по табл. 2). Так, символ пробела кодируется тремя двоичными символами, буква О – также тремя символами, и так далее, до буквы Ф, которая кодируется девятью двоичными символами. Расчеты дают значение mcp = 4,45 символов.
- число двоичных символов в коде Шеннона-Фэно данного j -го символа (считается по табл. 2). Так, символ пробела кодируется тремя двоичными символами, буква О – также тремя символами, и так далее, до буквы Ф, которая кодируется девятью двоичными символами. Расчеты дают значение mcp = 4,45 символов.
Деля энтропию Н на среднее число двоичных символов в расчете на одну букву, получим информацию в расчете на один двоичный символ I = H / mcp = 
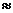 0,994 бита.
0,994 бита.
Полученное для упрощенного русского алфавита значение величины информации в расчете на один двоичный символ, как видно, весьма близко к единице, то есть выбранный код весьма близок к оптимальному. Количество информации в расчете на один двоичный символ было бы равно точно одному биту в том случае, если бы при каждом разбиении совокупностей символов на две группы суммарные частоты появления символов из этих двух групп всегда были бы точно равны друг другу.
Однако побуквенное кодирование по методу Шеннона-Фано имеет существенный недостаток. Если в процессе кодирования, передачи и декодирования сообщения произойдет хотя бы одна ошибка (например, символ 0 заменится на символ 1), то очень часто становится невозможным декодировать не только тот символ алфавита, в двоичном коде которого допущена ошибка, но и весь дальнейший текст.
Метод Хаффмана
Способ оптимального префиксного построения двоичных кодов с минимальной избыточностью предложил Д. Хаффман. Рассмотрим этапы его реализации.
Пусть Х={х1,..., хm} — входной алфавит кода F, а В={0,1} — выходной алфавит. С каждым сообщением хi связана вероятность рi, его появления. Необходимо каждому символу алфавита Х сопоставить кодовую комбинацию в алфавите В таким образом, чтобы обеспечить минимальную избыточность кода F.
Представленная задача решается путем построения кодового дерева. Построение его графа начинается с висячих вершин, которым в качестве весов назначают вероятности рi, i=1,..., т. Висячие вершины графа упорядочивают в соответствии с их весом. Это позволяет в дальнейшем уменьшить число пересечений ребер или совсем исключить их. В начале построения имеется т изолированных вершин графа, являющихся поддеревьями и одновременно корнями поддеревьев. Далее дерево строится по следующему алгоритму.
1) Определяется число поддеревьев графа. Если оно меньше двух, то дерево построено и на этом действие алгоритма заканчивается. Если число поддеревьев равно или больше двух, то переходят ко второму этапу.
2) Выбираются корни двух поддеревьев графа с минимальными весами и осуществляется сращивание выбранных поддеревьев с добавлением при этом двух ребер и одной вершины. Вес вновь образованной вершины определяется как сумма весов корней выбранных поддеревьев. Левому добавленному ребру приписывается вес, равный нулю, правому — равный единице. Далее возвращаются к первому этапу.
В результате применения алгоритма образуется кодовое дерево — граф со взвешенными ребрами. Для получения кода сообщения х; достаточно выписать веса ребер, составляющих путь из корня дерева в соответствующую висячую вершину.
Пример. Разработать код с использованием метода Хаффмана для входного алфавита Х={xi,...,х8} и выходного алфавита В={0,1}, если сообщениям X1,...,х8 соответствуют следующие вероятности их появления:
Xi, Х1, Х2 Хз Х4 X5 Х6, Х7 Х 8
Рi, 0.19 0.16 0.16 0.15 0.12 0.11 0.09 0.02
Построим кодовое дерево (рис. 3).
Таким образом, кодовые комбинации выглядит следующим образом:
Х1 – 10; Х2 – 000; Х3 – 001; Х4 – 010; Х5 – 011; Х6 – 110; Х7 – 1110; Х8 – 1111.
При этом mср =2.92, Н(Х) = 2.85.
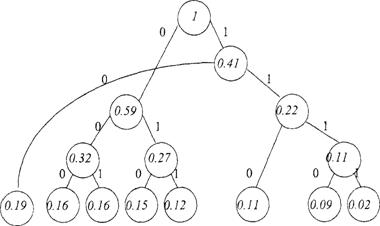
X1 Х2 Хз Х4 Х5 Х6 Х7 Х8
Рис. 3. Кодовое дерево, построенное по методу Хаффмана
Минимальная длина кодовой комбинации
Н(Х) 2.85
m min = ——— = ——— = 2,85
log2m log22
2.92 - 2.85
Коэффициент избыточности К = ——— —— = 0.023, то есть построенный код 2.92
практически не имеет избыточности.
Код Хаффмана важен в теоретическом отношении, поскольку доказано, что он является самым экономичным из всех возможных методов алфавитного кодирования, т. е. не существует другого алфавитного метода кодирования, длина кода которого меньше чем длина кода Хаффмана.
Этот метод нашел широкое применение в программах-архиваторах, программах резервного копирования дисков и файлов, в системах сжатия информации в модемах и факсах.
Не нашли, что искали? Воспользуйтесь поиском: