Логические операции и таблицы истинности

Отрицание высказывания Ā является простым высказыванием. Оно истинно, когда А ложно, и ложно, когда А истинно.

Таблица истинности – это табличное представление логической операции, в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

Составное высказывание, образованное в результате логического умножения (конъюнкции, лат. conjunctio – соединение), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания (табл. 1). Пусть А - высказывание: «У больного повышенная температура», а В - «У больного повышенное давление». Тогда А∧В будет высказыванием «У больного повышенная температура и повышенное давление».

Таблица 1. Таблица истинности логического умножения

Составное высказывание, образованное в результате логического сложения (дизъюнкции, лат. disjunction – разделение) истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний (табл. 2).

Если за А взять высказывание «Предвиденный диагноз - ангина», а за

В взять высказывание «катар верхних дыхательных путей», то A ∨ B является высказыванием «Предвиденный диагноз (ангина или катар верхних дыхательных путей».

Таблица 2. Таблица истинности логического сложения

Последовательность выполнения операций при отсутствии скобок в сложных логических формулах определяется старшинством операций (приоритетом). Наивысший приоритет имеет отрицание, затем следует конъюнкция и, наконец, дизъюнкция.

Употребляя введенные логические операции, можно, подобно к тому как это делается алгебре с помощью символов «+»,- строить сколько угодно сложные выражения. Рассмотрим высказывание: “При открытом переломе таза имеются повреждения внешних тканей тела (кожи), сильная боль в участке таза, невозможность самостоятельно встать или сесть”.

Сделаем следующие обозначения: пусть

А – наличие повреждения внешних тканей тела (кожи);

В – сильная боль в участке таза;

С – невозможность самостоятельно встать;

К – невозможность самостоятельно сесть

1 – открытый перелом таза;

Тогда сложная формула (А∧В∧ (С∨К)) = 1 является сокращенной записью рассмотренного высказывания.

Диаграммы Венна

Диаграммы Венна является графическим представлением всех возможных объектов, которые принадлежат к некоторому классу. (рис. 1). Прямоугольником в диаграмме Венна обозначают область некоторого класса объектов, а конкретный класс обозначают кругом.

Возьмем для примера, класс животных. Этот класс может визуализироваться всеми объектами в пределах прямоугольника - млекопитающие, рыбы, и т.п.. Если мы хотим в пределах класса представить, например, млекопитающих, то подаем всех млекопитающих в пределах круга, а других животные - извне. На рисунке 1 изображенные диаграммы Вена, для логических операций возражения

(случай (а)), дизъюнкции (случай (b)), конъюнкции (случай (с)).

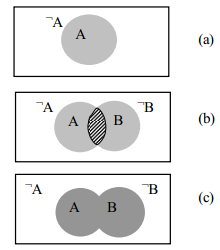
Рис 1. Диаграммы Венна

Случай (а) иллюстрирует операцию возражения: область высказывания А обозначено кругом, тогда А, за определением, - область извне круга. Если высказывание А приобретает значение ИСТИНА, то А − ЛОЖЬ, и наоборот. Заштрихованная область случая (b) указывает область высказывания A ∧ B, а случая (с) иллюстрирует действие операции А∨В.

Не нашли, что искали? Воспользуйтесь поиском: