
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретические основы. Первый подход к формализации алгоритма связан с формализацией понятия вычислителя, т
Первый подход к формализации алгоритма связан с формализацией понятия вычислителя, т. е. к построению очень простого, но функционально полного вычислителя. Таким вычислителем является машина Тьюринга.
Неформальное описание.
Машина Тьюринга состоит из:
- бесконечной в обе стороны ленты;
- вычислительной головки.

В каждый момент времени (такт) головка находится в некотором состоянии и обозревает одну позицию на ленте, в которой находится символ (обозреваемый символ).
Головка может выполнить одно из четырех действий:
1) Записать в обозреваемую позицию на ленте новый символ.
2) Переместиться на одну позицию влево по ленте.
3) Переместиться на одну позицию вправо по ленте.
4) Больше ничего не делать.
Действие головки однозначно определяется парой: (<текущее состояние головки> <обозреваемый символ>) и задается программой. Если в программе текущая пара не существует, то головка останавливается.
 Практические задания
Практические задания
1. Какую функцию вычисляет машина Т со следующей программой:
q10 → q20R,
q11 → q01,
q20 → q01,
q21 → q21R?
2. Построить машину Тьюринга (представить программу в виде таблицы и в форме диаграммы) для решения следующих задач:
3. Прибавить 1 к целому неотрицательному числу (вычислить функцию F (x) = x + 1).
Рассмотреть задачу для машины Тьюринга с алфавитами
a. A = {0, 1, e } (операции выполняются в двоичной системе);
b. A = {1, e } (строка «… e 1 e …» соответствует x = 0, в записи любого другого целого числа x > 0 количество единиц равно x + 1).
4. Вычесть 1 из целого неотрицательного числа (вычислить функцию F (x) = x – 1). Операции выполняются по следующему правилу:
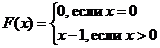 .
.
Рассмотреть задачу для машины Тьюринга с алфавитами
a. A = {0, 1, e } (операции выполняются в двоичной системе);
b. A = {1, e } (строка «… e 1 e …» соответствует записи x = 0 на ленте, в записи любого другого целого числа x > 0 количество единиц равно x + 1).
5. Прибавить 3 к целому неотрицательному числу (вычислить функцию F (x) = x + 3).
Построить решение в двух вариантах:
a. машина Тьюринга строится для вычисления указанной функции;
b. машина Тьюринга строится как композиция машин Тьюринга, вычисляющих функции F (x) = x + 1 и F (x) = x + 2.
6. Умножить на 2 целое положительное число x (вычислить функцию F (x) = 2× x)).
Числа записываются в двоичной системе (используется алфавит A = {0, 1, e }).
7. Умножить на 2 целое положительное число (вычислить функцию F (x) = 2× x). Для записи чисел используется алфавит A = {1, e } (строка «… e 1 e …» соответствует записи x = 0 на ленте, в записи любого другого целого числа x > 0 количество единиц равно x + 1) ***.
8. Умножить на 4 целое положительное число, записанное в двоичной системе (вычислить функцию F (x) = 4× x).
a. машина Тьюринга строится для вычисления указанной функции;
b. машина Тьюринга строится как композиция машин Тьюринга, вычисляющих функции F (x) = 2× x.
9. Умножить на степень 2 (на 2 n) целое положительное число x (вычислить функцию F (x, n) = 2 n × x)).
Числа записываются в двоичной системе (используется алфавит A = {0, 1, e, Ä}).
На ленте числа x и n записываются последовательно и разделяются символом ‘Ä’. В результате выполнения программы машины Тьюринга на ленте должно остаться одно число – результат умножения ***.
10.  На ленте записано целое число (используется двоичная система счисления, значение может быть как положительным, так и отрицательным, отрицательное значение записывается в прямом коде со знаком минус, перед положительным числом может стоять знак плюс, т.е. используется алфавит A = {0, 1, e, +, –}). Написать программу машины Тьюринга для вычисления функций ***
На ленте записано целое число (используется двоичная система счисления, значение может быть как положительным, так и отрицательным, отрицательное значение записывается в прямом коде со знаком минус, перед положительным числом может стоять знак плюс, т.е. используется алфавит A = {0, 1, e, +, –}). Написать программу машины Тьюринга для вычисления функций ***
a. F (x) = x + 1 (увеличения на 1 к записанного на ленте числа);
b. F (x) = x – 1 (вычитания 1 из записанного на ленте числа).
11.  Напишите рекурсивную процедуру закраски фигуры. Используется два цвета (цвет границ фигур и цвет закраски). Покажите порядок закраски по шагам (постройте дерево вызова и выполните «заливку» (до 15 вызова процедуры), используя приведенную ниже схему). Начальная точка отмечена буквой “ x ” (первый вызов процедуры выполняется для точки с координатами, соответствующими выделенной на схеме клетке), каждой точке на экране соответствует элемент матрицы на схеме:
Напишите рекурсивную процедуру закраски фигуры. Используется два цвета (цвет границ фигур и цвет закраски). Покажите порядок закраски по шагам (постройте дерево вызова и выполните «заливку» (до 15 вызова процедуры), используя приведенную ниже схему). Начальная точка отмечена буквой “ x ” (первый вызов процедуры выполняется для точки с координатами, соответствующими выделенной на схеме клетке), каждой точке на экране соответствует элемент матрицы на схеме:
| х | ||||||||||||||||
| х | ||||||||||||||||
| х | ||||||||||||||||
Контрольные вопросы
1. Какие существуют машины, кроме Тьюринга?
2. Как можно проверить работу машины?
Список литературы
| 1.Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с. | |
| 2.Варпаховский Ф.Л. Элементы теории алгоритмов. - М., Просвещение, 1970. - 25 с. (МГЗПИ) | |
| 3.Гуц А.К. Математическая лоrика и теория алrоритмов. - Омск: Издательство Наследие. Диалог-Сибирь, 2003. - 108 с. | |
| 4.Босс В. Лекции по математике. Т. 6: От Диофанта до Тьюринга. - М.: КомКнига, 2006. - 208 с. | |
| 5.Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. - 216 с. |
Не нашли, что искали? Воспользуйтесь поиском: