
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Организация ветвлений
Очень распространенной задачей является программирование процессов с несколькими исходами – ветвящихся процессов.
Задача 1. Для произвольного аргумента Х вычислить значение кусочно-ломаной функции Y(X) (рис. 2).
 |

 Одно из возможных решений задачи приведено на рис. 3 и 4. Здесь имена переменных отображены строчными буквами, а ключевые слова – прописными только для наглядности. Как уже указывалось, регистр букв безразличен – в Бейсике они воспринимаются одинаково.
Одно из возможных решений задачи приведено на рис. 3 и 4. Здесь имена переменных отображены строчными буквами, а ключевые слова – прописными только для наглядности. Как уже указывалось, регистр букв безразличен – в Бейсике они воспринимаются одинаково.
|
Здесь используется помеченный оператор (2 PRINT y). Необходимость в этом возникла вследствие потребности перейти к печати от операторов IF, минуя оператор y=10-0.5*x. В данном случае метка может быть любым числом, а не только 2. Замечание. В блок-схеме, на связях имеющих очевидное направление, стрелки можно не указывать.
Отметим, что практически любая задача может быть запрограммирована различными способами. Например, здесь возможно и такое решение.
INPUT x
IF x<0 THEN y=5+x: PRINT y: END
IF x<10 THEN y=5: PRINT y: END
y=10-0.5*x: PRINT y
Задача 2. Даны три произвольных числа А, В, С. Составить программу, которая анализирует их и, если сумма первых двух чисел не меньше третьего, а второе число больше первого – выдает сообщение ВЕРНО. Если хотя бы одно из условий не выполняется – то сообщение НЕВЕРНО. Иными словами
 “ВЕРНО” если А+В>=C и В>A
“ВЕРНО” если А+В>=C и В>A
“НЕВЕРНО” – в противном случае
На рис. 5 и 6 представлено решение (блок-схема и программа), полностью адекватное условию. Однако в некоторых случаях решение удобно искать, преобразовав условие на обратное, т.е.
 “НЕВЕРНО” если А+В<C или В<=A
“НЕВЕРНО” если А+В<C или В<=A
“ВЕРНО” – в противном случае
Это позволяет иногда упростить программирование (рис. 7).
При необходимости выполнять анализ одновременно нескольких условий удобно воспользоваться логическими функциями. Аргументами логических функций являются высказывания, в отношении которых всегда можно сказать, истинны они или ложны. К таким высказываниям относятся математические операции сравнения – равно, больше, меньше и т.д. Так, например, выражение вида Х=Y всегда может быть только истинным или только ложным. Рассмотрим важнейшие логические функции (см. таблицу ниже).
Функция одного аргумента НЕ истинна тогда и только тогда, когда ложен ее аргумент. То есть значение функции всегда обратно аргументу. Поведение функции полностью описывает таблица. В операторе IF функция И обозначается словом NOT. Например, следующие два оператора полностью идентичны
IF X<10 THEN Y=5 IF NOT X>=10 THEN Y=5
| Аргумент | Функция НЕ | Первый аргумент | Второй аргумент | Функция И | Функция ИЛИ | |
| Ложь | Истина | Ложь | Ложь | Ложь | Ложь | |
| Истина | Ложь | Ложь | Истина | Ложь | Истина | |
| Истина | Ложь | Ложь | Истина | |||
| Истина | Истина | Истина | Истина |
Из функций двух аргументов для нас важны функции И и ИЛИ. Функция И истинна тогда и только тогда, когда истинны все ее аргументы (в программах обозначается словом AND). Функция ИЛИ (OR) истинна тогда, когда истинен хотя бы один из ее аргументов. Если нет скобок, функции вычисляются в такой последовательности: НЕ, И, ИЛИ.
В качестве примера снова рассмотрим задачу 2 в исходной формулировке. Теперь ее решение сводится практически к одной строке и приведено ниже
INPUT a,b,c
IF a+b>=c AND b>a THEN? “Верно” ELSE? “Неверно”
Другой пример. Для А,В,С выяснить, правда ли что первое число самое большое, а последнее – самое маленькое.
IF a>b AND a>c AND c<a AND c<b THEN? “Верно” ELSE? “Неверно”
Еще. Верно ли, что среди чисел имеется ровно одна единица?
IF (a=1 AND b<>1 AND c<>1) OR (a<>1 AND b=1 AND c<>1)
OR (a<>1 AND b<>1 AND c=1) THEN? “Верно” ELSE? “Неверно”
Здесь скобки введены лишь для наглядности, поскольку операция AND все равно выполняется прежде операции OR.
Пример. Написать программу, которая для любого года G определяет високосный он или нет (ответ ДА/НЕТ). Подсказка: признаком високосного года является кратность года числу 4. Исключением являются года с двумя нулями на конце, число сотен в которых не кратно 4 (например, 1800, 1900, 2100). Кратность чисел можно определять с помощью функции FIX или операции MOD.
INPUT g
IF (g MOD 4=0) AND NOT((g MOD 100=0) AND (g/100 MOD 4<>0)) THEN? “Да” ELSE? “Нет”
Разъясним цепочку анализа. Год должен быть кратным четырем (g MOD 4=0), кроме случая (AND NOT), когда год имеет два нуля в конце (g MOD 100=0) и число сотен, в котором не кратно четырем AND (g/100 MOD 4<>0).
@ Задачи для самостоятельного решения. Напишите программу, выясняющую следующие факторы:
1). Даны три произвольных числа А, В, С. Выяснить правда ли что числа расположены в порядке возрастания их значений? Ответы должны быть даны словами: Да/Нет.
2). Даны А, В, С. Выяснить правда ли что среди чисел имеются отрицательные (хотя бы одно)? Ответы – Да/Нет.
3). Выяснить правда ли что среди чисел А, В, С имеются одинаковые? Ответы – Да/Нет.
4). Найти наибольшее из чисел А, В, С. Здесь удобно использовать три оператора IF, каждый из которых проверяет на максимум одно из чисел. Если данное число оказалось самым большим, следует его напечатать и сразу прекратить вычисления оператором END включенным внутрь структуры IF.
5). Вывести число, занимающее промежуточное положение между самым большим и самым маленьким из чисел А,В,С.
6). На плоскости нарисован прямоугольник. Напишите программу, которая для точки с произвольными координатами Х и Y определяет факт ее попадания внутрь прямоугольника. Ответ – Да/Нет. Положение квадрата указано на рисунке. Кроме того, вычислить площадь прямоугольника S.
7). Для той же фигуры определить факт ее попадания точки в область j или k или вне квадрата. Ответ должен быть дан в виде цифр 1, 2 или фразы «Вне квадрата».
8). На плоскости проведена прямая. Определить в какую из областей j, k, l, m попала наша точка.
 9). На плоскости проведены две прямых линии. Определить, попала ли точка внутрь заштрихованной области. Ответ дать в форме Да/Нет.
9). На плоскости проведены две прямых линии. Определить, попала ли точка внутрь заштрихованной области. Ответ дать в форме Да/Нет.
10). Положим, автомобиль был взят на прокат с датой G1, M1, H1, Min1 (год, месяц, день, час, минуты), а был возвращен в G2, M2, H2, Min2. Вычислить сколько времени использовался автомобиль T (в часах и минутах), а также, сколько должен заплатить клиент за использование автомобиля при часовом тарифе 100 руб/час. Длительность всех месяцев считать равной 30 дням.
11). Те же условия, но длительность каждого месяца брать фактической (с учетом високосности года). Считать также, что событие может происходить в период (2006-2009гг).
12). То же, но до 2050 года.
Организация циклов
В простых примерах, рассмотренных выше, вообще говоря, не требовалось привлечения ЭВМ и программирования. Все они достаточно быстро могли быть решены вручную или с помощью калькулятора. Сила ЭВМ заключается в возможности простыми средствами осуществлять многократное повторение заданных действий – циклов.
Итерационные циклы. В случае если количество циклов, необходимых для решения задачи, заранее неизвестно, такие циклы называются итерационными. Рассмотрим ряд примеров.

Задача 3. Пусть для некоторого множества чисел Х нужно вычислить и отпечатать функцию 2/Х. Ввод и вычисления следует прекратить после обнаружения первого Х, равного нулю (деление на ноль невозможно).
| Программа | Проверка | ||||
| к задаче 4 | 1 цикл | 2 цикл | 3 цикл | 4 цикл | |
| x=3 2 IF x>9 GOTO 4 y=(x–6)^2 ? x,y x=x+2 GOTO 2 4 END | x=3
 x=3<9
y=9
3,9
x=3+2=5 x=3<9
y=9
3,9
x=3+2=5
| 5<9 y=1 5,1 x=7 | 7<9 y=1 7,1 x=9 | 9=9 y=9 9,9 x=11 | 11>9 конец |
Очевидна следующая (рис. 8а) блок-схема. Блоков ввода, вычисления, печати и анализа столько, сколько чисел в последовательности до первого нуля. Чисел может быть очень много и подобный подход, конечно, неприемлем, не говоря уже о том, что и количество их заранее неизвестно. Такие программы строятся по-иному. Обрабатывающая часть программы записывается только раз, но охватывается петлей возврата (рис. 8б). Тогда одни и те же операторы будут выполняться многократно до тех пор, пока Х¹0.
Задача 4. Пусть для аргумента Х, находящегося в диапазоне от 3 до 9, требуется вычислить и напечатать значение функции Y=(X–6)2, где Х изменяется с шагом 2 (рис. 9а). Блок-схема алгоритма изображена на рис. 9б.
Справа от текста программы сделаны выкладки по проверке решения. В каждой строке вручную вычисляется и указывается значение соответствующей переменной. Выкладки по проверке выполняются сверху-вниз, слева-направо по ходу исполнения программы. Стрелки показывают связи между циклами. Видим, что заданная последовательность изменения Х (3, 5, 7,...) наблюдается и последнее значение Y вычисляется для Х=9. При следующем приращении Х оно становится равным 11 и пятый цикл не выполняется, поскольку при Х>9 программа завершается.
Здесь следует отметить, что нет никакого технически простого способа предварительной проверки правильности написанных программ. Для этой цели программисту приходится вручную по тексту программы рассчитывать значения всех переменных и сличать их с желаемыми (известными из условия). Конечно, проверка выполняется не для всей задачи, а только для небольшого числа (например, трех) начальных циклов и при этом тщательно анализируется значение условия выхода из цикла (оператор IF).
@ Задачи для самостоятельного решения. Напишите программы:
1). Решите задачу 4 для Х, изменяющегося в обратном направлении (9¸3).
2). Вычислить и напечатать значения функции Y=10–2X для последовательных значений Х: 0, 0.5, 1, 1.5, 2, 2.5,... и т.д. до тех пор, пока Y не станет отрицательным.
3). Решите задачу 3, где вычисления Y прекращаются после того, как будут встречены три числа Х<0. Указание. Здесь понадобится переменная – счетчик таких значений. Назовем ее К. Следует прекратить вычисления при К=3.
Арифметические циклы. Если число повторений известно заранее – такие циклы называются арифметическими.
Задача 5. Пусть в условиях предыдущей задачи 4 не известно предельное значение аргумента, но зато задано количество точек аргумента – 4. Поскольку в данном случае не задано последнее значение Х, признак окончания циклов придется формировать самим. Для этого вводится переменная, которая фиксирует число уже выполненных циклов, т.е. счетчик циклов (назовем ее I). В исходном состоянии (рис. 10) берем его равным 1.
 |
| Программа | Проверка | ||||
| к задаче 5 | 1 цикл | 2 цикл | 3 цикл | 4 цикл | |
| x=3: i=1 8 IF i>4 GOTO 2 y=(x–6)^2 ? x y x=x+2 i=i+1 GO TO 8 2 END | x=3, i=1
 i=1<4
y=9
3, 9
x=5
i=2 i=1<4
y=9
3, 9
x=5
i=2
| 2<4 y=1 5, 1 x=7 | 3<4 y=1 7, 1 x=9 | 4=4 y=9 9, 9 x=11 | 5>4 конец |
После выполнения очередного цикла счетчик получает приращение, увеличиваясь на единицу (I=I+1). В начале каждого цикла в операторе IF делается проверка на достижение счетчиком последнего разрешенного значения (у нас 4). Если I<=4 программа продолжает вычисление функции, если нет (I>4) – счет прекращается. Ниже приведена программа и выкладки по ее проверке. Как видим, результат проверки совпал с результатом, полученным ранее.
| Программа | Проверка для N=3 X=2,4,3 | |||
| к задаче 6 | 1 цикл | 2 цикл | 3 цикл | |
| INPUT “N=”,n i=1: s=0 3 IF i>n GOTO 8 INPUT “X=”,x s=s+x i=i+1 GOTO 3 8 PRINT s | n=3
i=1, s=0
 1<3
x=2
s=2
i=2 1<3
x=2
s=2
i=2
| 2<3 | 3=3 | 4>3 s=9 |
Исходное значение счетчика циклов и его приращения могут выглядеть по-разному. Главное, чтобы было выполнено заданное число циклов. В нашем примере был использован счетчик на возрастание I=1,2,3,... до N (N – число шагов). Можно начинать счетчик с нуля: I=0,1,2,... до N-1. Возможен счетчик на убывание: I=N–1,... 3,2,1 до 0 и т.д. Обычно, если нет оснований для другого, используется счетчик на возрастание с шагом единица от 1 до N.
@ Задачи для самостоятельного решения.
1). Решите задачу 5 для Х, изменяющегося в обратном направлении (Х начинается с 9).
2). Напечатайте цепочку из 10-ти чисел Х, изменяющихся по закону: 2, 6, 18, 54….
Задачи на накопление. В практике очень распространены задачи на накопление, т.е. на нахождение сумм и произведений последовательности переменных. Такие задачи могут встречаться как в формулировке итерационных, так и арифметических циклов.
Задача 6. Пусть требуется найти сумму N произвольных чисел Х. Блок-схема алгоритма приведена на рис. 11, а программа ниже. Здесь сумма накапливается в переменной S с помощью оператора S=S+X. Начальное значение суммы берется равным нулю (S=0).
Числовые ряды. Типичной циклической задачей на накопление является вычисление числовых рядов.
Задача 7. Пусть требуется найти сумму S для N членов геометрической прогрессии вида
| Программа | Проверка | для N=3 | ||
| к задаче 7 | 1 цикл | 2 цикл | 3 цикл | 4 цикл |
| INPUT n | n=3 | |||
| a=3: i=1: s=0 | a=3, i=1,s=0 | |||
| 3 IF i>n GOTO 9 |  i=1<3 i=1<3
| 2<3 | 3=3 | 4>3 |
| s=s+a | s=0+3=3 | 3+6=9 | 9+12=21 | |
| a=2*a | a=2*3=6 | |||
| i=i+1 | i=1+1=2 | |||
| GOTO 3 | ||||
| 9? s | s=21 |
A1 A2 A3 A4 N
 S = 3 + 6 + 12 + 24 +... + = åАi
S = 3 + 6 + 12 + 24 +... + = åАi
S1 S2 S3 S4
Здесь каждый следующий член прогрессии Аi равен предыдущему Ai+1, умноженному на два. Если учесть введенные обозначения, можно записать так называемые рекуррентные формулы
 Si= Si–1+ Ai, где Sо = 0
Si= Si–1+ Ai, где Sо = 0
Ai= 2Ai–1 A1= 3
Или, как принято в программировании
 S=0, S=S+A
S=0, S=S+A
A=3, A=2A
Аналогично строятся программы для циклического произведения, однако исходное значение искомого произведения берется равным единице. Если действовать по аналогии с суммой и сделать его равным нулю, результат всегда будет также нулем, поскольку умножение на нуль дает только нуль.
@ Задачи для самостоятельного решения.
1). Найдите произведение N элементов ряда: Y=3×6×12×24×....
2). Найдите сумму N элементов ряда: Y=–3+6–12+24–….
3). Найдите сумму N элементов ряда: Y=–2+4–6+12–….
Указание. В задаче 2) каждый новый элемент может быть получен умножением предыдущего на минус два (–2) поскольку здесь наблюдается геометрическая прогрессия. Для формирования изменяющегося знака в задаче 3) с арифметической прогрессией такой подход не сработает. Придется формировать знак отдельно. Здесь удобно ввести специальную переменную Z, равную то +1, то –1 на которую будет умножаться очередной элемент ряда. Первоначальное значение Z определяется знаком при первом элементе ряда. У нас будет Z=–1. Далее эта переменная должна меняться по закону Z=–Z. Таким образом, Z будет то –1 то +1, что при перемножении на элемент ряда будет каждый раз менять его знак на противоположный.

Оператор арифметического цикла. Принципы построения программ с арифметическими циклами можно проиллюстрировать обобщенной блок-схемой на рисунке 12.
Группа операторов внутри цикла называется телом цикла. Только обрабатывающая часть цикла полезна. Остальные операторы являются обслуживающими, необходимыми для организации цикла. Этот механизм в алгоритмических языках обычно реализует специальный оператор цикла, который мы сейчас рассмотрим. Его применение упрощает программирование и снижает возможность совершения ошибок.
Структура вида:
| ü | FOR | изменяемая переменная | = | начальное значение | TO | конечное значение | STEP шаг |
Операторы в цикле
NEXT
последовательно выполняет операторы, находящиеся между оператором FOR до оператора NEXT столько раз, сколько нужно для того, чтобы изменяемая переменная от начального значения достигла конечного значения с установленным шагом.
Например:
FOR a = 3 TO 7.5 STEP 0.8
Операторы
NEXT a
Здесь группа операторов от оператора FOR до оператора NEXT будет повторяться столько раз, сколько нужно, чтобы переменная А, изменяясь с шагом 0.8 от значения равного 3, достигла 7.5. Таким образом, мы последовательно получим: A=3; 3.8; 4.6; 5.4; 6.2; 7, т.е. цикл будет выполнен 6 раз. При следующем значении А=7.8 циклы более не выполняются, поскольку А становится больше предельно возможного (7.8>7.5) в данном операторе FOR. Далее программа продолжаться с оператора, следующего сразу после NEXT.
В качестве параметров оператора цикла разрешены выражения. Например: FOR c=b+2 TO k STEP x–2. Если шаг изменения переменной цикла 1, разрешается его не указывать. Так, операторы
FOR i=4 TO k STEP 1 и FOR i=4 TO k
полностью эквивалентны. Дословно такой оператор интерпретируется следующим образом: “Выполнять операторы цикла от оператора FOR до оператора NEXT столько раз, сколько нужно, чтобы переменная I, изменяясь с шагом 1, достигла значения k.” Цикл перестанет выполняться в момент, когда переменная цикла становится больше предельного значения цикла (k).
 Допускается отрицательный шаг и превышение начального значения цикла над конечным, например
Допускается отрицательный шаг и превышение начального значения цикла над конечным, например
FOR i=20 TO 10 STEP -3
Здесь переменная I последовательно получит значения: 20, 17, 14, 11.
После слова NEXT обычно, но необязательно, указывается имя изменяемой переменной цикла (переменной, следующей непосредственно после слова FOR), что позволяет легко контролировать правильное закрытие циклов. Для простых (невложенных) циклов имя переменной можно не указывать.
Оператор цикла является сильнейшим средством программиста. Он один заменяет несколько операторов в цикле, построенном обычным образом – это операторы задания исходного значения циклической переменной (или счетчика циклов) и операторы ее приращения и анализа. Оператор FOR удобен для реализации арифметических циклов.
На блок-схемах оператор FOR отображается в виде фигуры “прямоугольник в ромбе”, которая имеет два выхода. Выход ДА соответствует случаю, когда переменная цикла меньше или равна своему предельному значению – цикл продолжает выполняться. Выход НЕТ – случаю превышения переменной этой границы – цикл завершается. Иногда можно воспользоваться упрощенным обозначением цикла FOR, когда он включается в виде заголовка в прямоугольник, содержащий операторы цикла. К такой форме возможно прибегать, если тело цикла не содержит разветвлений или собственных циклов.
| Программа к | Проверка для N=3 | |||
| задаче 7 (с FOR) | 1 цикл | 2 цикл | 3 цикл | |
| INPUT n a=3: s=0 FOR i=1 TO n s=s+a a=2*a NEXT ? s | n=3 a=3, s=0 i=1<3 s=0+3=3 a=2*3=6 | 2<3 | 3=3 | 4>3 s=21 |
Решим задачу 7 с применением оператора FOR. Здесь необходимо просуммировать в переменную S все числа Х из множества N чисел. Блок-схема приведена на рис. 13а и 13б в обоих возможных вариантах. Второй более компактен, однако, как уже говорилось, он возможен не всегда.
Если необходимо выйти из цикла FOR до его естественного завершения (до выполнения всех циклов), можно применить оператор GOTO, но удобнее воспользоваться специальным оператором выхода вида
üEXIT FOR
который передает управление на оператор, следующий непосредственно за оператором NEXT.
Если нужно, не выполняя до конца текущего цикла, начать следующий, следует перейти оператором GOTO непосредственно на оператор NEXT. В задаче 8, например, это оператор IF x<0 THEN s=s+x: GOTO 9.
Задача 8. Для N произвольных чисел Х вычислить и отпечатать: сумму отрицательных чисел S, количество положительных КР, произведение положительных чисел Р. Все вычисления производить до появления первого нуля в последовательности. Если нуль не встретился, кроме S, KP и Р напечатать сообщение НУЛЕЙ НЕТ. Блок-схема алгоритма приведена на рис. 14. В программе сделана проверка для N=5 и чисел Х=3,–2,1,–3,2. В результате получено S=–5, P=6, KP=3.
| Программа | Проверка для N=5 | |||||
| к задаче 8 | 1 цикл | 2 цикл | 3 цикл | 4 цикл | 5 цикл | |
| INPUT n kp=0: s=0: p=1 FOR i=1 TO n INPUT x IF x=0 GOTO 7 IF x<0 THEN s=s+x: GOTO 9 kp=kp+1 p=p*x 9 NEXT ?“Нулей нет” 7? s p kp | n=4 i=1<5 x=3 x≠0 x>0 kp=1 p=3 | 2<5 x=-2 x≠0 x<0, s=-2 | 3<5 x=1 x≠0 x>0 kp=2 p=3 | 4<5 x=-3 x≠0 x<0, s=-5 | 5=5 x=2 x≠0 x>0 kp=3 p=6 Нулей | 6>5 нет -5,6,3 |
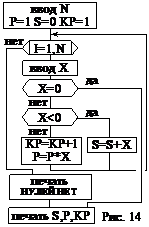
Задача 9. Для чисел Х и Y найти наибольший общий делитель, т.е. такое наибольшее число, которое делит X и Y без остатка. Например, для 24 и 12 НОД=12, для 12 и 18 НОД=6. Нахождение НОД будем выполнять путем последовательного перебора сверху вниз всех натуральных чисел от минимального из X и Y до 1. Наибольшим общим делителем считаем первое значение i, которое делит оба числа без остатка.
Не нашли, что искали? Воспользуйтесь поиском: