
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тест №14 Механические колебания и волны
Тест №14 Механические колебания и волны
Задание 5 № 602. Шарик колеблется на пружине, подвешенной вертикально к потолку, при этом максимальное расстояние от потолка до центра груза равно H, минимальное h. В точке, удаленной от потолка на расстояние h:
1) кинетическая энергия шарика максимальна 2) потенциальная энергия пружины минимальна
3) потенциальная энергия взаимодействия шарика с землей максимальна
4) потенциальная энергия взаимодействия шарика с землей минимальна
Решение.
В точке, удаленной от потолка на расстояние h, шарик меняет направление своего движения. Он перестает подниматься и начинает опускаться, поэтому скорость его в этой точке равна нулю, а значит, кинетическая энергия минимальна. С другой стороны, в этой точке шарик находится на максимальной высоте над поверхностью земли, следовательно, потенциальная энергия взаимодействия шарика с землей максимальна.
Правильный ответ: 3.
Примечание
Необходимо отметить, что потенциальная энергия пружины минимальна, когда пружина не растянута. Если просто подвесить груз к потолку на пружине, пружина растянется, и при колебаниях груз будет колебаться вокруг этого нового «растянутого» положения равновесия. Поэтому если окажется так, что h в точности совпадает с длиной недеформированной пружины, то в этой точке пружина будет не растянута. Следовательно, при таком условии пункт 2 также будет верен.
Задание 5 № 607. На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени.
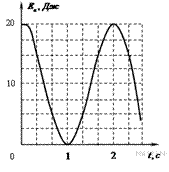
В момент времени 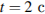 кинетическая энергия маятника равна:
кинетическая энергия маятника равна:
1) 0 Джтт2) 8 Дж 3) 16 Дж 4) 32 Дж
Решение.
При колебании математического маятника выполняется закон сохранения полной механической энергии, так как на маятник не действует никаких внешних сил, совершающих работу. В любой момент времени имеем
 .
.
Из графика видно, что в момент времени 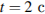 потенциальная энергия достигает максимума и совпадает со значением полной механической энергии. Следовательно, в этот момент времени кинетическая энергия обращается в ноль. В итоге, имеем
потенциальная энергия достигает максимума и совпадает со значением полной механической энергии. Следовательно, в этот момент времени кинетическая энергия обращается в ноль. В итоге, имеем
 .
.
Правильный ответ: 1.
Задание 5 № 3630. 
Груз колеблется на пружине, двигаясь вдоль оси  . На рисунке показан график зависимости координаты груза
. На рисунке показан график зависимости координаты груза  от времени
от времени 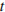 . На каких участках графика сила упругости пружины, приложенная к грузу, совершает положительную работу?
. На каких участках графика сила упругости пружины, приложенная к грузу, совершает положительную работу?
1) 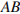 и
и 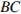 2)
2) 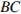 и
и  3)
3) 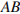 и
и  4)
4) 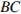 и
и 
Решение.
Сила упругости, действующая со стороны пружины на груз, всегда направлена против деформации пружины. Работа силы положительна, когда направление силы совпадает с направлением перемещения тела. Если груз отклоняется от положения равновесия, он тормозится, сила упругости совершает отрицательную работу. Наоборот, если тело возвращается в положение равновесия, его скорость увеличивается, сила упругости совершает положительную работу. Таким образом, для того, чтобы ответить на вопрос, на каких участках графика сила упругости пружины, приложенная к грузу, совершает положительную работу, необходимо отобрать все участки, на которых тело приближается к положению равновесия, то есть участки 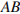 и
и  .
.
Правильный ответ: 3.
Задание 5 № 5499.  При гармонических колебаниях пружинного маятника координата груза
При гармонических колебаниях пружинного маятника координата груза  изменяется с течением времени t, как показано на рисунке. Период Т и амплитуда колебаний А равны соответственно
изменяется с течением времени t, как показано на рисунке. Период Т и амплитуда колебаний А равны соответственно
1) T = 4 с, A = 1,5 см 2) Т = 5 с, А = 1,5 см 3) T = 3 с, A = 3 cм 4) T = 2 c, A = 3 cм
Решение.
Период колебаний — это время, за которое маятник совершает одно полное колебание, оно составляет 4 с.
Амплитуда колебаний — это максимальное отклонение от положения равновесия  она равна 1,5 см.
она равна 1,5 см.
Правильный ответ указан под номером 1.
Задание 5 № 6148. Маятники 1 и 2 совершают гармонические колебания по законам x 1(t) = 6cos3 t и x 2(t) = 12sin3 t. Фазы колебаний этих маятников
1) одинаковые 2) отличаются в 2 раза 3) отличаются в 4 раза 4) отличаются на 
Решение.
Воспользуемся формулами приведения:

Следовательно фазы колебаний этих маятников отличаются на 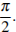
Правильный ответ указан под номером: 4.
Задание 5 № 6336.  Маленький грузик, закреплённый на пружине жёсткостью 80 Н/м, совершает гармонические колебания. График зависимости координаты x этого грузика от времени t изображён на рисунке. Масса грузика равна
Маленький грузик, закреплённый на пружине жёсткостью 80 Н/м, совершает гармонические колебания. График зависимости координаты x этого грузика от времени t изображён на рисунке. Масса грузика равна
1) 20 г 2) 25 г 3) 40 г 4) 50 г
Решение.
Период колебаний пружинного маятника  Из графика находим, что период колебаний равен
Из графика находим, что период колебаний равен  Найдём массу груза:
Найдём массу груза:


Правильный ответ указан под номером: 4.
Задание 5 № 626. Человеческое ухо воспринимает звуковые волны, длины которых лежат в интервале от 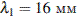 до
до  . Отношение граничных частот звуковых волн
. Отношение граничных частот звуковых волн  этого интервала равно
этого интервала равно
1)  2)
2)  3)
3) 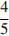 4)
4) 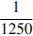
Решение.
Частота, длина и скорость распространения звуковых волн связаны соотношением  Отсюда находим отношение граничных частот волн
Отсюда находим отношение граничных частот волн
 .
.
Правильный ответ: 1.
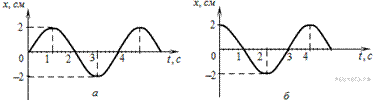
Задание 5 № 713. На графиках представлена зависимость координаты х центров масс тела а и тела б от времени t при гармонических колебаниях вдоль оси Ox.

На каком расстоянии друг от друга находятся центры масс тел а и б в момент времени 0 с?
1) 4 см 2) 2 см 3) 0 см 4)  2 см
2 см
Решение.
Из представленных графиков видно, что в момент времени 0 с тело а находилось в положении равновесия  , а тело б отклонилось на максимальное расстояние:
, а тело б отклонилось на максимальное расстояние:  Таким образом, в момент времени 0 с центры масс тел а и б отстояли друг от друга на расстоянии
Таким образом, в момент времени 0 с центры масс тел а и б отстояли друг от друга на расстоянии
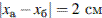 .
.
Правильный ответ: 2.
Задание 5 № 4191. На рисунке изображён участок натянутого резинового шнура, по которому распространяется поперечная волна, имеющая частоту 1,25 Гц. Чему равна скорость распространения волны?
 1) 0,8 м/с 2) 0,4 м/с 3) 0,625 м/с 4) 1,25 м/с
1) 0,8 м/с 2) 0,4 м/с 3) 0,625 м/с 4) 1,25 м/с
Решение.
Скорость распространения волны связана с частотой и длиной волны соотношением  . На рисунке изображено 3/4 периода, следовательно, длина волны равна
. На рисунке изображено 3/4 периода, следовательно, длина волны равна  . Таким образом, скорость распространения волны равна
. Таким образом, скорость распространения волны равна  .
.
Правильный ответ: 4
Задание 5 № 4342. Точечное тело совершает гармонические колебания вдоль оси ОХ. На рисунке изображена зависимость смещения х этого тела от времени t. Проекция скорости тела на ось ОХ положительна в точках
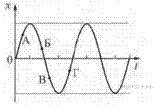 1) А и Б 2) В и Г 3) А и Г 4) Б и В
1) А и Б 2) В и Г 3) А и Г 4) Б и В
Решение.
Скорость — это производная от координаты по времени. На графике 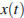 скорости соответствует тангенс угла наклона графика. Следовательно, положительным значениям проекции скорости тела на ось OX отвечают такие точки на графике, которым соответствует положительный наклон касательной. Это точки А и Г.
скорости соответствует тангенс угла наклона графика. Следовательно, положительным значениям проекции скорости тела на ось OX отвечают такие точки на графике, которым соответствует положительный наклон касательной. Это точки А и Г.
Правильный ответ: 3
Задание 6 № 2605. Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой 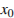 . Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
. Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;2) уменьшилась; 3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная энергия пружины | Частота колебаний |
Решение.
Период колебаний связан с массой груза и жесткостью пружины k соотношением  . При уменьшении массы период колебаний уменьшится. Частота обратно пропорциональна периоду, значит, частота увеличится.
. При уменьшении массы период колебаний уменьшится. Частота обратно пропорциональна периоду, значит, частота увеличится.
С максимальной потенциальной энергией пружины все немного сложнее. Для ответа на вопрос, что с ней произойдет существенно, что пружина ориентирована вертикально (для горизонтального пружинного маятника при неизменной амплитуде данная величина, естественно, останется неизменной). Действительно, когда к вертикальной пружине подвешивают груз, она сразу немного растягивается, чтобы уравновесить силу тяжести, действующую на груз. Определим это начальное растяжение:  . Именно это состояние является положением равновесия для вертикального пружинного маятника, колебания происходят вокруг него, груз поднимается и опускается из этого положения на величину амплитуды. При движении вниз из положения равновесия пружина продолжает растягиваться, а значит, потенциальная энергия пружины продолжает увеличиваться. При движении вверх из положения равновесия, сперва деформация пружины уменьшается, а если
. Именно это состояние является положением равновесия для вертикального пружинного маятника, колебания происходят вокруг него, груз поднимается и опускается из этого положения на величину амплитуды. При движении вниз из положения равновесия пружина продолжает растягиваться, а значит, потенциальная энергия пружины продолжает увеличиваться. При движении вверх из положения равновесия, сперва деформация пружины уменьшается, а если  , то пружины начнет сжиматься. Максимальной потенциальной энергии пружины соответствует состояние, когда она максимально растянута, а значит, в нашем случае, это положение, когда груз опустился максимально вниз. Таким образом, максимальная потенциальная энергия пружины равна
, то пружины начнет сжиматься. Максимальной потенциальной энергии пружины соответствует состояние, когда она максимально растянута, а значит, в нашем случае, это положение, когда груз опустился максимально вниз. Таким образом, максимальная потенциальная энергия пружины равна
 .
.
Из этой формулы видно, что для вертикального пружинного маятника при неизменной амплитуде и уменьшении массы груза максимальная потенциальная энергия пружины уменьшится.
Спрятать решение
Задание 6 № 2609. Груз изображенного на рисунке пружинного маятника совершает гармонические колебания между точками 1 и 3. 
Как меняются кинетическая энергия груза маятника, скорость груза и жесткость пружины при движении груза маятника от точки 1 к точке 2?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается; 2) уменьшается; 3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Кинетическая энергия груза маятника | Скорость груза | Жесткость пружины |
Решение.
Точка 2 представляет собой положение устойчивого равновесия маятника. Когда груз находится в точке 2, пружина не деформирована. Точка 1, напротив, соответствует сжатой пружине. При движении груза от точки 1, в которой он имеет нулевую скорость, к точке 2, пружина разжимается, ускоряя груз. Таким образом, на этой фазе колебания скорость груза увеличивается. Кинетическая энергия пропорциональна квадрату скорости: 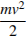 , — следовательно, кинетическая энергия груза также увеличивается. Жесткость пружины является характеристикой пружины, не зависящей от фазы колебания, поэтому жесткость пружины не изменяется.
, — следовательно, кинетическая энергия груза также увеличивается. Жесткость пружины является характеристикой пружины, не зависящей от фазы колебания, поэтому жесткость пружины не изменяется.
Ответ: 113.
Задание 6 № 3892. 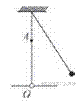 Маленький шарик, подвешенный на лёгкой нерастяжимой нити, совершает колебания. Когда шарик проходит положение равновесия, с помощью специального зажима, расположенного в точке А, изменяют положение точки подвеса. Как при этом изменяются следующие физические величины: период колебаний шарика, амплитуда колебаний шарика, модуль силы натяжения нити в точке О?
Маленький шарик, подвешенный на лёгкой нерастяжимой нити, совершает колебания. Когда шарик проходит положение равновесия, с помощью специального зажима, расположенного в точке А, изменяют положение точки подвеса. Как при этом изменяются следующие физические величины: период колебаний шарика, амплитуда колебаний шарика, модуль силы натяжения нити в точке О?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается; 2) уменьшается; 3) не изменяется. Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | |
| A) Период колебаний шарика Б) Максимальный угол отклонения шарика от положения равновесия B) Модуль силы натяжения нити в точке О | 1) Увеличивается 2) Уменьшается 3) Не изменится |
| A | Б | В |
Решение.
Период колебаний математического маятника связан с длиной подвеса и ускорением свободного падения соотношением:  . Таким образом, если изменить точку подвеса так, как показано на картинке, период колебаний уменьшится (А — 2).
. Таким образом, если изменить точку подвеса так, как показано на картинке, период колебаний уменьшится (А — 2).
Выпишем второй закон Ньютона для шарика в точке О в проекции на вертикальную ось:  . Ускорение
. Ускорение  есть центростремительное ускорение движения по окружности. Как известно, оно связано со скоростью движения и радиусом окружности соотношением:
есть центростремительное ускорение движения по окружности. Как известно, оно связано со скоростью движения и радиусом окружности соотношением: 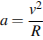 . При перемещении точки подвеса маятника в точку
. При перемещении точки подвеса маятника в точку 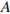 скорость движения шарика в точке
скорость движения шарика в точке  не изменится, а вот радиус окружности, по которой двигается шарик, уменьшится. Следовательно, ускорение шарика в точке
не изменится, а вот радиус окружности, по которой двигается шарик, уменьшится. Следовательно, ускорение шарика в точке  увеличится. Отсюда сразу видим,что и сила натяжения нити в этой точке увеличится:
увеличится. Отсюда сразу видим,что и сила натяжения нити в этой точке увеличится:  (В — 1).
(В — 1).
 При колебания выполняется закон сохранения полной механической энергии. При перемещении точки подвеса в точку
При колебания выполняется закон сохранения полной механической энергии. При перемещении точки подвеса в точку 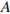 энергия так же не изменяется. Поэтому максимальная высота подъема шарика над положением равновесия в результате такого изменения останется той же. Но так как длина подвеса уменьшилась, легко заметить, что максимальный угол отклонения теперь будет больше, то есть амплитуда колебаний увеличится (Б — 1).
энергия так же не изменяется. Поэтому максимальная высота подъема шарика над положением равновесия в результате такого изменения останется той же. Но так как длина подвеса уменьшилась, легко заметить, что максимальный угол отклонения теперь будет больше, то есть амплитуда колебаний увеличится (Б — 1).
Правильный ответ: 211
Задание 6 № 7177. На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:
1) увеличится 2) уменьшится 3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Глубина погружения бруска | Сила Архимеда |
Решение.
Так как брусок плавает на поверхности воды, то сила тяжести уравновешена силой Архимеда:  . Учитывая, что
. Учитывая, что  , можем переписать данное выражение в виде:
, можем переписать данное выражение в виде:  . Видно, что при изменении массы тела и постоянстве прочих параметров, равновесие сохранится, значит глубина погружения не изменится.
. Видно, что при изменении массы тела и постоянстве прочих параметров, равновесие сохранится, значит глубина погружения не изменится.
Замена бруска бруском такой же плотности, но большей массы, означает, что новый брусок имеет больший объем, а значит сила Архимеда, действующая на него будет больше.
Ответ: 31.
Задание 6 № 5739.  Небольшой брусок, насаженный на гладкую спицу, прикреплён к пружине, другой конец которой прикреплён к вертикальной опоре. Брусок совершает гармонические колебания. В некоторый момент времени всю систему начинают перемещать с постоянным ускорением в положительном направлении оси Ох. Как при этом изменяются следующие физические величины: частота колебаний бруска, период колебаний бруска, координата его положения равновесия.
Небольшой брусок, насаженный на гладкую спицу, прикреплён к пружине, другой конец которой прикреплён к вертикальной опоре. Брусок совершает гармонические колебания. В некоторый момент времени всю систему начинают перемещать с постоянным ускорением в положительном направлении оси Ох. Как при этом изменяются следующие физические величины: частота колебаний бруска, период колебаний бруска, координата его положения равновесия.
1) увеличилась 2) уменьшилась 3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ |
| А) Частота колебаний бруска | 1) увеличится |
| Б) период колебаний бруска | 2) уменьшится |
| В) Координата его положения равновесия | 3) не изменится |
| A | Б | В |
Решение.
Частота гармонических колебаний пружинного маятника зависит только от коэффициента жёсткости пружины и массы грузика:  поэтому при ускоренном передвижении частота колебаний не изменится. А — 3).
поэтому при ускоренном передвижении частота колебаний не изменится. А — 3).
Период колебаний есть обратная частота, поэтому он не изменится. Б — 3).
Исходная система отсчёта становится неинерциальной, поэтому на грузик будет действовать инерциальная сила, направленная в противоположную сторону от оси Ox, следовательно, координата положения равновесия будет уменьшится. В — 2).
Ответ: 332.
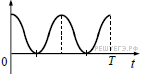
Задание 7 № 6507. 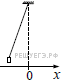 Груз, привязанный к нити, отклонили от положения равновесия и в момент t = 0 отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
Груз, привязанный к нити, отклонили от положения равновесия и в момент t = 0 отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | |
А)
 Б)
Б)

| 1) координата х 2) проекция скорости vх 3) кинетическая энергия Е к 4) потенциальная энергия Е п |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б |
Решение.
Координата и скорость изменяются циклически по синусоидальном закону. В начальный момент времени координата отрицательна, а скорость равна нулю, поэтому ни один из графиков не может являться графиком скорости. Поскольку скорость в начальный момент времени равна нулю, кинетическая энергия в начальный момент времени также равна нулю. Координата может принимать как положительные, так и отрицательные значения, следовательно, под буквой Б указан график зависимости координаты от времени. Методом исключения получаем, что под буквой А указан график потенциальной энергии.
Ответ: 41.
Тест №14 Механические колебания и волны
1.Задание 5 № 602. Шарик колеблется на пружине, подвешенной вертикально к потолку, при этом максимальное расстояние от потолка до центра груза равно H, минимальное h. В точке, удаленной от потолка на расстояние h:
1) кинетическая энергия шарика максимальна 2) потенциальная энергия пружины минимальна
3) потенциальная энергия взаимодействия шарика с землей максимальна
4) потенциальная энергия взаимодействия шарика с землей минимальна
2.Задание 5 № 607. На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени.
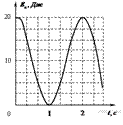
В момент времени 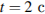 кинетическая энергия маятника равна 1) 0 Джтт2) 8 Дж 3) 16 Дж 4) 32 Дж
кинетическая энергия маятника равна 1) 0 Джтт2) 8 Дж 3) 16 Дж 4) 32 Дж
3.Задание 5 № 3630. 
Груз колеблется на пружине, двигаясь вдоль оси  . На рисунке показан график зависимости координаты груза
. На рисунке показан график зависимости координаты груза  от времени
от времени 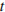 . На каких участках графика сила упругости пружины, приложенная к грузу, совершает положительную работу?
. На каких участках графика сила упругости пружины, приложенная к грузу, совершает положительную работу?
1) 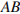 и
и 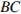 2)
2) 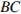 и
и  3)
3) 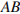 и
и  4)
4) 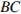 и
и 
4. Задание 5 № 5499.  При гармонических колебаниях пружинного маятника координата груза
При гармонических колебаниях пружинного маятника координата груза  изменяется с течением времени t, как показано на рисунке. Период Т и амплитуда колебаний А равны соответственно
изменяется с течением времени t, как показано на рисунке. Период Т и амплитуда колебаний А равны соответственно
1) T = 4 с, A = 1,5 см 2) Т = 5 с, А = 1,5 см 3) T = 3 с, A = 3 cм 4) T = 2 c, A = 3 cм
5. Задание 5 № 6148. Маятники 1 и 2 совершают гармонические колебания по законам x 1(t) = 6cos3 t и x 2(t) = 12sin3 t. Фазы колебаний этих маятников
1) одинаковые 2) отличаются в 2 раза 3) отличаются в 4 раза 4) отличаются на 
6. Задание 5 № 6336.  Маленький грузик, закреплённый на пружине жёсткостью 80 Н/м, совершает гармонические колебания. График зависимости координаты x этого грузика от времени t изображён на рисунке. Масса грузика равна
Маленький грузик, закреплённый на пружине жёсткостью 80 Н/м, совершает гармонические колебания. График зависимости координаты x этого грузика от времени t изображён на рисунке. Масса грузика равна
1) 20 г 2) 25 г 3) 40 г 4) 50 г
7.Задание 5 № 626. Человеческое ухо воспринимает звуковые волны, длины которых лежат в интервале от 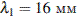 до
до  . Отношение граничных частот звуковых волн
. Отношение граничных частот звуковых волн  этого интервала равно
этого интервала равно
1)  2)
2)  3)
3) 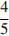 4)
4) 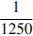
8.Задание 5 № 713. На графиках представлена зависимость координаты х центров масс тела а и тела б от времени t при гармонических колебаниях вдоль оси Ox.
На каком расстоянии друг от друга находятся центры масс тел а и б в момент времени 0 с?
1) 4 см 2) 2 см 3) 0 см 4)  2 см
2 см
9.Задание 5 № 4191. На рисунке изображён участок натянутого резинового шнура, по которому распространяется поперечная волна, имеющая частоту 1,25 Гц. Чему равна скорость распространения волны?
 1) 0,8 м/с 2) 0,4 м/с 3) 0,625 м/с 4) 1,25 м/с
1) 0,8 м/с 2) 0,4 м/с 3) 0,625 м/с 4) 1,25 м/с
10 Задание 5 № 4342. Точечное тело совершает гармонические колебания вдоль оси ОХ. На рисунке изображена зависимость смещения х этого тела от времени t. Проекция скорости тела на ось ОХ положительна в точках
 1) А и Б 2) В и Г 3) А и Г 4) Б и В
1) А и Б 2) В и Г 3) А и Г 4) Б и В
11.Задание 6 № 2605. Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой 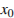 . Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
. Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;2) уменьшилась; 3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная энергия пружины | Частота колебаний |
| Кинетическая энергия груза маятника | Скорость груза | Жесткость пружины |
12.Задание 6 № 2609. Груз изображенного на рисунке пружинного маятника совершает гармонические колебания между точками 1 и 3. 
Как меняются кинетическая энергия груза маятника, скорость груза и жесткость пружины при движении груза маятника от точки 1 к точке 2?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается; 2) уменьшается; 3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
13.Задание 6 № 3892.  Маленький шарик, подвешенный на лёгкой нерастяжимой нити, совершает колебания. Когда шарик проходит положение равновесия, с помощью специального зажима, расположенного в точке А, изменяют положение точки подвеса. Как при этом изменяются следующие физические величины: период колебаний шарика, амплитуда колебаний шарика, модуль силы натяжения нити в точке О?
Маленький шарик, подвешенный на лёгкой нерастяжимой нити, совершает колебания. Когда шарик проходит положение равновесия, с помощью специального зажима, расположенного в точке А, изменяют положение точки подвеса. Как при этом изменяются следующие физические величины: период колебаний шарика, амплитуда колебаний шарика, модуль силы натяжения нити в точке О?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается; 2) уменьшается; 3) не изменяется. Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ | |||||||
A) Период колебаний шарика Б) Максимальный угол отклонения шарика от положения равновесия
B) Модуль силы натяжения нити в точке О | 1) Увеличивается 2) Уменьшается 3) Не изменится |
Задание 6 № 7177. На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:
1) увеличится 2) уменьшится 3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Глубина погружения бруска | Сила Архимеда |
Задание 6 № 5739.  Небольшой брусок, насаженный на гладкую спицу, прикреплён к пружине, другой конец которой прикреплён к вертикальной опоре. Брусок совершает гармонические колебания. В некоторый момент времени всю систему начинают перемещать с постоянным ускорением в положительном направлении оси Ох. Как при этом изменяются следующие физические величины: частота колебаний бруска, период колебаний бруска, координата его положения равновесия.
Небольшой брусок, насаженный на гладкую спицу, прикреплён к пружине, другой конец которой прикреплён к вертикальной опоре. Брусок совершает гармонические колебания. В некоторый момент времени всю систему начинают перемещать с постоянным ускорением в положительном направлении оси Ох. Как при этом изменяются следующие физические величины: частота колебаний бруска, период колебаний бруска, координата его положения равновесия.
1) увеличилась 2) уменьшилась 3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИХ ИЗМЕНЕНИЕ |
| А) Частота колебаний бруска | 1) увеличится |
| Б) период колебаний бруска | 2) уменьшится |
| В) Координата его положения равновесия | 3) не изменится |
| A | Б | В |
Задание 7 № 6507.  Груз, привязанный к нити, отклонили от положения равновесия и в момент t = 0 отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
Груз, привязанный к нити, отклонили от положения равновесия и в момент t = 0 отпустили из состояния покоя (см. рисунок). На графиках А и Б показано изменение физических величин, характеризующих движение груза после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
 ГР ГР  АФИКИ АФИКИ
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | |||||
| А) Б) | 1) координата х 2) проекция скорости vх 3) кинетическая энергия Е к
4) потенциальная энергия Е п |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| <== предыдущая лекция | | | следующая лекция ==> |
| а.5 Система надбавок, доплат та премій працівникам | | | Классификация расстройств психики, возникающих при чрезвычайных ситуациях |
Не нашли, что искали? Воспользуйтесь поиском: