Графическое решение задач математического программирования.

Рассмотрим ЗМП с двумя неизвестными:

- целевая функция - система ограничений

1) Строим ОДР задачи.

Областью решения каждого из неравенств будет часть плоскости, ограниченная линией . Очевидно, что решением системы неравенств будет пересечение всех их областей решений. ОДР задачи МП – общая часть областей решений всех неравенств системы ограничений.

Если ОДР – пустое множество, задача не имеет решения в силу несовместности системы ограничений.

Если ОДР – непустое множество, задача может иметь одно или бесконечное множество решений.

2) Строим линии уровня целевой функции (линии, в которых значение функции постоянно).

=С –уравнения линий уровня.

Если Z – линейная функция, то её линии уровня – семейство прямых, перпендикулярных вектору градиенту этой функции.

Вектором градиентом функции называется вектор 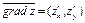, координаты которого равны частным производным этой функции. Вектор градиент показывает направление максимального возрастания значения функции.

3) Двигаясь от одной линии уровня к другой в направлении вектора градиента (в задачах на максимум) или в противоположном направлении (в задачах на минимум), находим опорную кривую.

Опорная кривая _ такая линия уровня, которая имеет хотя бы одну общую точку с ОДР, и, при этом, не разделяет её на части.

4) Находим оптимальное решение задачи – общие точки ОДР и опорной кривой.

Не нашли, что искали? Воспользуйтесь поиском: