Находим начальное опорное решение.

[составляем симплекс таблицу,

преобразуем расширенную матрицу уравнений ограничений методом Жордано – Гаусса, разрешаем её относительно m базисных переменных, выбранных произвольно, но с соблюдением условия неотрицательности,

приравниваем свободные переменные к нулю, вычисляем значения базисных переменных,

находим значение целевой функции для найденного начального опорного решения].

3) Проверяем найденное опорное решение на оптимальность.

[ заполняем первые два столбца симплекс таблицы,

вычисляем оценки векторов столбцов коэффициентов при свободных переменных (см. ниже),

проверяем выполнение признаков оптимальности и единственности найденного решения:

если все оценки столбцов свободных переменных положительны, найден максимум ЗЛП,

если все оценки столбцов свободных переменных отрицательны, найден минимум ЗЛП,

если хотя бы одна из оценок столбцов свободных переменных равна нулю, решений бесконечно много, они находятся по формуле , где находим путём перебора всех опорных решений ЗЛП].

Вычисление оценки разложения вектора условий по базису опорного решения.

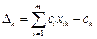или ,

где - вектор – столбец коэффициентов целевой функции при базисных переменных, - вектор – столбец коэффициентов системы ограничений при k-ой переменной, - коэффициент в целевой функции при k-ой переменной.

Признаки оптимальности решения ЗЛП, найденного симплекс методом.

Допустимое решение ЗЛП на максимум является оптимальным,

если оценки всех векторов столбцов коэффициентов неотрицательны.

[ЗЛП на максимум - ].

Допустимое решение ЗЛП на минимум является оптимальным, если оценки всех векторов столбцов коэффициентов не положительны [ЗЛП на минимум - ].

Оценки всех базисных столбцов равны 0.

Признак единственности решения ЗЛП, найденного симплекс методом.

Если оценки всех свободных векторов-столбцов не равны нулю, найденное оптимальное решение единственно.

4) Если оптимальное решение не найдено, ищем новое опорное решение.

Признак отсутствия оптимального решения в силу неограниченности целевой функции.

ЗЛП не имеет решения в силу неограниченности целевой функции, если какой-нибудь столбец коэффициентов свободной переменной, оценка которого противоречит признаку оптимальности, не содержит ни одного положительного элемента.

Если условие отсутствия оптимального решения не выполняется, введём в базис новую переменную, столбец коэффициентов которой имеет оценку, противоречащую признаку оптимальности. Если таких столбцов несколько, выбираем столбец с «наихудшей» оценкой.

Для выбора разрешающего элемента в столбце новой базисной переменной используем условие неотрицательности свободных членов. Из базиса выводится столбец с разрешающим элементом (единицей) в соответствующей строке.

Получив новое опорное решение, вычисляем соответствующее ему значение целевой функции.

Приращение целевой функции при переходе от одного опорного решения к другому можно вычислить по формуле:

5. Постановка и основные понятия транспортной задачи.

Транспортные задачи – целочисленные задачи линейного программирования в канонической форме, коэффициенты при переменных в ограничениях равны нулю или единице и каждая переменная входит в систему ограничений два раза. Эти задачи можно решать обычным симплекс-методом, но мы рассмотрим более удобные специальные методы решения транспортных задач.

Дано: Несколько (m) поставщиков однородного товара хотят передать этот товар нескольким (n) потребителям. Мощность i го поставщика - равна запасам товара у этого поставщика. Мощности поставщиков заносятся в первый столбец таблицы поставок. Мощность j -го потребителя - - определяется количеством необходимого ему товара. Мощности потребителей равны их запросам. Известна стоимость перевозки единицы товара от каждого из поставщиков к каждому потребителю - .

Задача: Для каждой пары «поставщик-потребитель» определить объём перевозки , то есть составить оптимальный план перевозок товара.

Полученная матрица перевозок должна удовлетворять следующим условиям:

1) суммарные затраты на перевозку минимальны;

(Сумма затрат на перевозку равна сумме произведений объёмов перевозок товара на их стоимости )

2) мощности всех поставщиков реализованы;

3) запросы всех потребителей удовлетворены

В транспортной задаче n+m уравнений ограничений, n.m переменных; из них n+m+1 линейно независимых уравнений и n+m+1 базисных переменных (заполненных клеток в таблице поставок). Число свободных клеток n.m – (n+m+1) равно числу свободных переменных задачи.

Необходимое и достаточное условие существования решения транспортной задачи.

Суммарные запасы (мощности) поставщиков и потребителей равны между собой (задача закрыта, или задача с правильным балансом).

Цикл клетки (i,j) – последовательность клеток таблицы ТЗ, определяемая ломаной линией, состоящей из вертикальных и горизонтальных звеньев. Начало и конец ломаной – в клетке (i,j), остальные вершины – в заполненных клетках таблицы.

Допустимое решение ТЗ является базисным тогда и только тогда, когда из заполненных им клеток таблицы нельзя образовать ни одного цикла.

Алгоритм решения ТЗ,

1) находим начальное базисное допустимое (опорное) решение, состоящее из (n+m+1) заполненных клеток таблицы поставок методом северо-западного угла или методом минимальной стоимости. Убеждаемся в его «опорности» методом вычёркивания рядов с одной заполненной клеткой из матрицы поставок.

2) проверяем оптимальность найденного решения (используя различные критерии оптимальности)

3) если найденное решение не оптимально, изменяем его, используя «сдвиг по циклу»: увеличиваем объём перевозок во всех нечётных клетках цикла и уменьшаем во всех чётных на величину ( равен наименьшему из объёмов перевозок в чётных клетках цикла). Переходим к пункту 2).

Построение начального решения:

В клетку (i,j) таблицы поставок вносим максимально возможный объём перевозки, равный оставшимся запасам i-го поставщика или неудовлетворённым потребностям j -го потребителя. Затем вычёркиваем из таблицы поставщика или потребителя, потребности которого полностью удовлетворены. (одна заполненная клетка таблицы – один вычеркнутый ряд матрицы).

Метод северо-западного угла: последовательно заполняем правую верхнюю клетку таблицы поставок.

Метод минимальной стоимости – в первую очередь заполняем клетки с наименьшей стоимостью первозки.

Критерий оптимальности найденного решения распределительного метода.

Вычисляем оценку цикла для каждой свободной клетки таблицы поставок (складываем стоимости перевозок в нечётных клетках цикла и вычитаем стоимости в чётных клетках).

Если оценки циклов всех свободных клеток неотрицательны, найденное решение оптимально.

Критерий оптимальности найденного решения в методе потенциалов.

Вычисляем потенциалы строк и столбцов матрицы поставок из уравнений , составленных для каждой заполненной клетки таблицы.

Затем, по известным потенциалам и вычисляем оценки свободных клеток: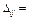

Если все оценки свободных клеток неположительны, то найденное решение оптимально.

Переход к новому решению:

Если обнаружена свободная клетка таблицы поставок, не удовлетворяющая критерию оптимальности, из неё строим цикл, вычисляем величину сдвига по циклу , если >0, осуществляем сдвиг по этому циклу и получаем новое опорное решение.

Не нашли, что искали? Воспользуйтесь поиском: