
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обчислення об’ємів тіл обертання
Нехай на відрізку 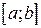 задана неперервна знакопостійна функція y=f(x). Об’єм Vx тіла, отриманого внаслідок обертання навколо осі Ох криволінійної трапеції, обмеженої лініями y=f(x), y =0; x=a; x=b (див мал. 2.8) обчислюється за формулою
задана неперервна знакопостійна функція y=f(x). Об’єм Vx тіла, отриманого внаслідок обертання навколо осі Ох криволінійної трапеції, обмеженої лініями y=f(x), y =0; x=a; x=b (див мал. 2.8) обчислюється за формулою
Vx =  . (2.4)
. (2.4)
Якщо криволінійну трапецію обертати навколо осі Оy (мал. 2.9), то Vy= 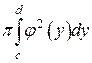 . (2.5)
. (2.5)

 Приклад 1. Обчислити площу фігури, обмеженої лініями, що задані рівняннями:
Приклад 1. Обчислити площу фігури, обмеженої лініями, що задані рівняннями:
а) у=х2, у= 0, х= 3;
б) у=х2- 2 х, у= 0;
в) у=х2-х- 2, у=х+ 1;
г) у=х 2+2, у =-2 х +10, у =0, х =0.
Розв’язання. а)Площу зображеної на мал.2.10. фігури обчислимо, застосувавши формулу (2.1). 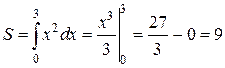 (кв.од.).
(кв.од.).
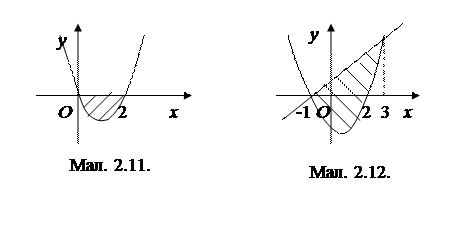 б) Фігура, площу якої треба знайти, розташована під віссю Ох (див. мал. 2.11.), тому скористаємося формулою (2.2).
б) Фігура, площу якої треба знайти, розташована під віссю Ох (див. мал. 2.11.), тому скористаємося формулою (2.2).
 .
.
в) Площу зображеної на малюнку 2.12. фігури обчислюємо, використовуючи формулу (2.3). Знайдемо межі інтегрування, якими є абсциси точок перетину прямої у=х +1 та параболи у=х2-х -2. Розв’язавши систему рівнянь 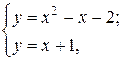 маємо х 1=-1; х 2=3. Отже,
маємо х 1=-1; х 2=3. Отже, 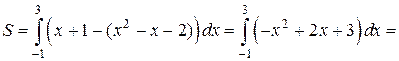
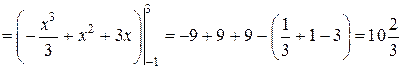 (кв.од.).
(кв.од.).
г) Розіб’ємо шукану площу на частини (див. мал. 2.13). Тобто SOABC=SOABD+SBCD. Абсциси точок А, В, С задають межі інтегрування. Зрозуміло, що абсциса точки А дорівнює нулю. Щоб знайти абсцису точки В, розв’яжемо систему рівнянь  Маємо х 1=-4; х 2=2. Нас задовольняє х 2=2. І, нарешті, знайдемо абсцису точки С. Покладемо у =0 в рівнянні прямої
Маємо х 1=-4; х 2=2. Нас задовольняє х 2=2. І, нарешті, знайдемо абсцису точки С. Покладемо у =0 в рівнянні прямої 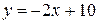 , маємо х =5. Отже,
, маємо х =5. Отже,  (кв.од.);
(кв.од.);
 (кв.од.).
(кв.од.).
Кінцевий результат: 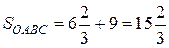 (кв.од.).
(кв.од.).
Приклад 2. Обчислити об’єм тіла, отриманого обертанням навколо осі Ох фігури, обмеженої лініями
а) y = 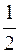 x +3, y =0, x =0, x =5;
x +3, y =0, x =0, x =5;
б) х=у 2-1, у=х -1.

Розв’язання. а) Зробимо малюнок (див. мал. 2.14). Застосовуючи формулу (2.4) обчислимо шуканий об’єм.
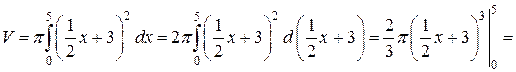
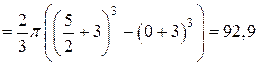 (од.3).
(од.3).
б) Виділимо штрихами на малюнку 2.15 фігуру, яка обертається. Легко бачити, що таке саме тіло обертання отримаємо, якщо навколо осі Ох обертати лише криволінійний трикутник PLM. Тоді шуканий об’єм дорівнює різниці Vx=VLMN-VPMN. Визначимо межі інтегрування, розв’язавши систему рівнянь 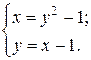 Отримуємо х 1=0, х 2=3. Нас задовольняє х 2=3. Застосувавши формулу (2.4), маємо:
Отримуємо х 1=0, х 2=3. Нас задовольняє х 2=3. Застосувавши формулу (2.4), маємо:

 .
.
 (од.3).
(од.3).
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Моему отцу и матери 1 страница |
Не нашли, что искали? Воспользуйтесь поиском: