JOptionPane.showMessageDialog(null, text);. По принятому в Java соглашению, ветвь else всегда относится к ближайшему предшествующему ему незанятому if:

}

}

По принятому в Java соглашению, ветвь else всегда относится к ближайшему предшествующему ему незанятому if:

== сравнения:

if (a==b)

System.out.printf(“\nЭти величины равны между собой”);

else System.out.printf(“\nЭти величины не равны между собой”);

Это правильное сравнение значений двух переменных.

Перепишем это сравнение с ошибкой:

if (a=b)

System.out.printf(“\nЭти величины равны между собой”);

else System.out.printf(“\nЭти величины не равны между собой”);

Компилятор обработает эту ошибку и выдаст сообщение:

Exception in thread "main" java.lang.RuntimeException: Uncompilable source code - incompatible types

required: boolean

found: double

at javaapplication1.JavaApplication1.main(JavaApplication1.java:25)

Здесь 25 – номер программной строки с ошибкой.

Часто встречающиеся ошибки программирования:

1. Использование else без первой ветви:

if (n > m)

Else...

2. Использование открывающей фигурной скобки { без закрывающей } и наоборот.

3. Отсутствие точки с запятой перед словом else:

4. Точка с запятой после условия:

if (n > m);

a=1;

else a=0;

5. Отсутствие точки с запятой перед закрывающей фигурной скобкой } или наличие точки с запятой после нее:

if (c < 2.5)

{

a=Math.sin(c);

b=Math.abs(c);

};

Else

{

a=Math.cos(c);

b=1.0/c

}

Пример

Задан график функции f(x) – полуокружность радиуса R=1:

Определить:

1. Значение функции y при заданном значении аргумента x.

2. Площади фигур слева и справа от линии разреза.

По теореме Пифагора:

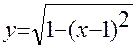
Площадь фигуры слева от линии разреза определяется суммой площадей прямоугольного треугольника:

s₁ = 0,5 x y

и сектора:

s₂ = 0,5 R² (α – sin α), где α – центральный угол в радианах,

причем

α = arcsin(y/R).

Площадь всей фигуры (полукруга) определяется выражением:

S = π R²/2.

Программа решения задачи:

Не нашли, что искали? Воспользуйтесь поиском: