
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методы обработки результатов наблюдений
Лекция4
Прямые измерения с многократными наблюдениями.
Методы обработки результатов наблюдений
Основной смысл усреднения многократных наблюдений одной и той же физической величины заключается в том, что найденная усредненная оценка координаты их центра имеет меньшую случайную погрешность, чем отдельные наблюдения, по которым она находится. Из сказанного следует, что усреднение не устраняет полностью случайный характер усредненного результата, а лишь уменьшает в какое-то число раз ширину полосы его неопределенности. Стремиться беспредельно уменьшать случайную погрешность результата измерения не имеет смысла, так как рано или поздно определяющим становится не рассеяние среднего арифметического, а недостоверность поправок на систематическую погрешность (неисключенная систематическая погрешность).
С целью приобретения практических навыков по методам обработки результатов прямых наблюдений предлагается использование задания в форме расчетно-графической работы или индивидуального задания на лабораторном практикуме.
Выбор задания осуществляется по 3-значному шифру. Первая цифра шифра – порядковый номер в списке потока или группы для данного студента, он же принимается за уровень напряжения, измеренного с помощью цифрового вольтметра.
С целью упрощения расчетов десятые и сотые доли результатов наблюдений для всех заданий взяты одинаковыми (табл. 2.4) при числе наблюдений
n = 20.
Пример. Результаты наблюдений, если студент в группе (потоке), числится под номером 12.
Таблица 2.4
| 12,42 | 12,43 | 12,42 | 12,39 | ||||
| 12,43 | 12,39 | 12,41 | 12,41 | ||||
| 12,40 | 12,45 | 12,39 | 12,43 | ||||
| 12,43 | 12,40 | 12,39 | 12,42 | ||||
| 12,42 | 12,43 | 12,40 | 12,48 |
Принимаем, что Dс в результатах наблюдений исключена за счет предварительного введения поправок, т.е. результаты
наблюдений – исправленные, однако, остается не исключенная составляющая q.
По второй цифре шифра из таблицы 2.5 выбирается класс точности (с/d) цифрового вольтметра (цв), с помощью которого измерялось напряжение.
Таблица 2.5
Класс точности цифровых вольтметров
| № варианта | ||||||||||
| с/d | 0,05 - 0,03 | 0,04 - 0,02 | 0,02 - 0,01 | 0,03 - 0,01 | 0,04 - 0,025 | 0,05 - 0,035 | 0,045 - 0,025 | 0,03 - 0,045 | 0,02 - 0,01 | 0,03 - 0,015 |
По третьей цифре шифра из таблицы 2.6 выбирается значение доверительной вероятности Р.
Таблица 2.6
Значения доверительной вероятности
| № | ||||||||||
| Р | 0,2 | 0,4 | 0,6 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,995 | 0,999 |
Конечной целью выполнения задания является нахождение результата измерения и представление его в форме записи:
 ,
,
где U – результат измерения;
 – средне арифметическое всех n наблюдений;
– средне арифметическое всех n наблюдений;
D U – погрешность измерения;
Р – доверительная вероятность.
В соответствии с правилами обработки результатов измерения с многократными наблюдениями алгоритм расчета будет следующим.
1. Вычисление среднего арифметического исправленных результатов измерений, принимаемое за результат измерений по формуле:
 , (2.21)
, (2.21)
где n – количество наблюдений;
Ui – отдельное наблюдение.
2. Вычисление оценки среднего квадратического отклонения (СКО) результатов наблюдения:

. (2.22)
3. Вычисление оценки среднего квадратичного отклонения результата измерения:

. (2.23)
4. Обозначим Vi = Ui -  как случайное отклонение.
как случайное отклонение.
Должно соблюдаться равенство
 .
.
Сведем результаты наблюдений и расчетов в таблицу 2.7
 .
.
5. Исключение из группы наблюдений анормальных результатов, содержащих грубые погрешности. Для этого из ряда значений Vi находим наибольшее и определяем отношение
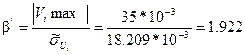 .
.
Таблица 2.7
Результаты расчётов
| № наблюдения | Результаты наблюдений | Случайное отклонение
Vi = Ui - 
| Квадраты случайных отклонений

|
| 12,42 | 0,005 | 25 
| |
| 12,43 | 0,015 | 225 
| |
| 12,40 | -0,015 | 225 
| |
| 12,43 | 0,015 | 225 
| |
| 12,42 | 0,005 | 25 
| |
| 12,43 | 0,015 | 225 
| |
| 12,39 | -0,025 | 625 
| |
| 12,45 | 0,035 | 1225 
| |
| 12,40 | -0,015 | 225 
| |
| 12,43 | 0,015 | 225 
| |
| 12,42 | 0,005 | 25 
| |
| 12,41 | -0,005 | 25 
| |
| 12,39 | -0,025 | 625 
| |
| 12,3940 | -0,025 | 625 
| |
| 12,40 | -0,015 | 225 
| |
| 12,39 | -0,025 | 625 
| |
| 12,41 | -0,005 | 25 
| |
| 12,43 | 0,015 | 225 
| |
| 12,42 | 0,005 | 25 
| |
| 12,44 | 0,025 | 625 
| |
| n = 20 |  =12,415 =12,415
| 
| 
|
Полученное значение  сравниваем со значением
сравниваем со значением  , взятым из таблицы 2.8. для данного объема выборки n = 20 и принятого уровня значимости q = 1– Р = 1– 0.95 = 0.05
, взятым из таблицы 2.8. для данного объема выборки n = 20 и принятого уровня значимости q = 1– Р = 1– 0.95 = 0.05
Из таблицы 2.8 получаем значение  = 2,623, что больше
= 2,623, что больше  . Следовательно, подозреваемый результат наблюдений (N =8) c Vi = 0.035 нормальным и его не исключают из выборки.
. Следовательно, подозреваемый результат наблюдений (N =8) c Vi = 0.035 нормальным и его не исключают из выборки.
В случае, если 
 , результат наблюдения был бы анормальным и его нужно было бы исключить из выборки.
, результат наблюдения был бы анормальным и его нужно было бы исключить из выборки.
Таблица 2.8
Значения  при различных числах наблюдений n
при различных числах наблюдений n
| n | q = 1 - P | n | q = 1 - P | ||||||
| 0,10 | 0,05 | 0,025 | 0,01 | 0,1 | 0,05 | 0,025 | 0,01 | ||
| 1,406 | 1,412 | 1,414 | 1,414 | 2,297 | 2,461 | 2,602 | 2,759 | ||
| 1,645 | 1,689 | 1,710 | 1,723 | 2,326 | 2,493 | 2,638 | 2,808 | ||
| 1,731 | 1,869 | 1,917 | 1,955 | 2,354 | 2,523 | 2,670 | 2,837 | ||
| 1,894 | 1,996 | 2,067 | 2,130 | 2,380 | 2,551 | 2,701 | 2,871 | ||
| 1,974. | 2,093 | 2,182 | 2,265 | 2,404 | 2,557 | 2,728 | 2,903 | ||
| 2,041 | 2,172 | 2,273 | 2,374 | 2,426 | 2,600 | 2,754 | 2,932 | ||
| 2,097 | 2,237 | 2,349 | 2,464 | 2,447 | 2,623 | 2,778 | 2,959 | ||
| 2,146 | 2,294 | 2,414 | 2,540 | 2,467 | 2,644 | 2,801 | 2,984 | ||
| 2,190 | 2,383 | 2,470 | 2,606 | 2,486 | 2,664 | 2,823 | 3,008 | ||
| 2,229 | 2,387 | 2,519 | 2,663 | 2,504 | 2,683 | 2,843 | 3,030 | ||
| 2,264 | 2,426 | 2,262 | 2,714 | 2,520 | 2,701 | 2,862 | 3,051 | ||
| 2,537 | 2,717 | 2,880 | 3,071 |
В таблице 2.8 q = 1 – P – уровень значимости (вероятность ошибки).
6. Проверка принадлежности результатов наблюдений нормальному закону распределения (НРЗ).
При числе наблюдений 50> n >15рекомендуется проверку на НЗР выполнять с помощью составного критерия, который фактически состоит из двух самостоятельных критериев.
Критерий 1
По данным случайных отклонений Ui находим отношение
 ,
,
где  – оценка квантилей распределения,
– оценка квантилей распределения,
S* – смещенная оценка результатов наблюдения, определяемая по формуле
 .
.
Тогда значение  будет равно
будет равно
 .
.
Затем выбираем уровень значимости в пределах q 1=(10-2) %. Берем q 1= 2 % и по таблице 2.9 находим значения квантилей  и
и  при n = 20,
при n = 20,
Результаты группы наблюдений можно считать распределенными нормально, если
 <
< 
 .
.
Т.к.  = 0,873, то 0,694 <
= 0,873, то 0,694 <  < 0,9, т.е. наблюдения распределены по НРЗ.
< 0,9, т.е. наблюдения распределены по НРЗ.
Таблица 2.9
Статистика d
| n | q 1/2 | (1- q 1/2)100 % | ||
| 1 % | 5 % | 95% | 99 % | |
| 0,9137 0,9001 0,8901 0,8826 0,8769 0,8722 0,8682 0,8648 | 0,8884 0,8768 0,8686 0,8625 0,8578 0,8540 0,8508 0,7518 | 0,7236 0,7304 0,7360 0,7404 0,440 0,7470 0,7496 0,7518 | 0,6829 0,6950 0,7040 0,7110 0,7167 0,7216 0,7256 0,7291 |
Критерий 2
Считают, что результаты наблюдений принадлежат НРЗ, если не более m разностей | Ui-U | превзошли значение ZР /2* S,
где 
ZP /2 – верхняя квантель распределения нормированной функции Лапласа, отвечающая вероятности Р /2.
Значения Р определяют из таблицы 2.10 по выбранному уровню значимости q 2 и числу результатов наблюдений n.
Таблица 2.10
Значения Р для вычисления ZР /2
| n | m | q 2*100 % | ||
| 1 % | 2 % | 5 % | ||
| 11-14 15-20 21-22 24-27 28-32 33-35 36-49 | 0,98 0,99 0,99 0,98 0,98 0,98 0,99 0,99 0,99 | 0,98 0,98 0,99 0,97 0,98 0,98 0,98 0,98 0,99 | 0,96 0,97 0,98 0,96 0,96 0,97 0,97 0,98 0,98 |
Выбрав q 2=5 % по таблице 2.10 при n =20 имеем Р =0,98 и m =1.
При этом для значения P /2 = 0,98/2 = 0,49 их таблицы 2.2 имеем ZР /2* S =
= 2,36*18,209*10-3 = 43*10-3 В, т.е. ни одна разность | Ui -  | не превзошла найденного значения 43*10-3 В (см. таблицу 2.7). Из этого следует, что оба критерия соблюдаются и, следовательно, распределение результатов наблюдений при n = 20 соответствует нормальному.
| не превзошла найденного значения 43*10-3 В (см. таблицу 2.7). Из этого следует, что оба критерия соблюдаются и, следовательно, распределение результатов наблюдений при n = 20 соответствует нормальному.
7. Определение случайной погрешности
Если имеем НЗР, то доверительные границы  (без учета знака) случайной составляющей
(без учета знака) случайной составляющей  погрешности результата измерения находим по формуле
погрешности результата измерения находим по формуле
 , (2.25)
, (2.25)
где  – Коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа наблюдений n находим из табл. 2.3.
– Коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа наблюдений n находим из табл. 2.3.
Примечание. С учебной целью, согласно шифру задания, значение Р берется из табл. 2.12
Таблица 2.12
| № вар. | ||||||||||
| Р | 0,2 | 0,4 | 0,6 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,995 | 0,999 |
Например, при Р = 0,9 и n – 1 = 19 из табл. 2.3 находим значение  =1,729, тогда
=1,729, тогда

8. Определение систематической погрешности
В начале задания было принято условие, что результаты наблюдений исправленные, однако остается неисключенная составляющая  . С учебной целью в качестве
. С учебной целью в качестве  берется погрешность цифрового вольтметра (ЦВ). Определим эту погрешность, учитывая, что класс точности ЦВ нормирован через относительную погрешность:
берется погрешность цифрового вольтметра (ЦВ). Определим эту погрешность, учитывая, что класс точности ЦВ нормирован через относительную погрешность:

(2.26)
где С/d – обозначение класса точности ЦВ;
Х К – предел измерения для данного диапазона измерения ЦВ;
Х – измеренное значение.
Для всех вариантов задания принимаем значение Х К на 10 % больше,
чем Х.
В общем случае относительная погрешность есть отношение абсолютной погрешности к измеренному значению, т.е. 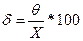 %.
%.
В нашем случае имеем 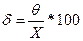 %. Отсюда
%. Отсюда  .
.
Например, если С/d = 0,02/0,01 и  = 12,412 В,
= 12,412 В,
то 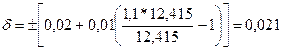 %,
%,
тогда  *10-3 В.
*10-3 В.
9. Условия определения границы погрешности результата измерения.
В случае, если 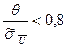 , то неисключенной систематической составляющей погрешности по сравнению со случайной пренебрегаем и принимаем, что граница погрешности результата измерения равна
, то неисключенной систематической составляющей погрешности по сравнению со случайной пренебрегаем и принимаем, что граница погрешности результата измерения равна
 (см. пункт 7).
(см. пункт 7).
Убеждаемся в справедливости этого:
 , то случайной погрешностью пренебрегаем по сравнению с
, то случайной погрешностью пренебрегаем по сравнению с  и принимаем, что граница погрешности результата измерения равна
и принимаем, что граница погрешности результата измерения равна  .
.
В случае, если вышеприведенные неравенства не выполняются, границу погрешности результата измерения находим путем построения композиции распределений случайных и неисключенных систематических погрешностей.
Если доверительные границы случайной погрешности найдены по выражению
 , то допускаются границы погрешности результата измерения (без учета знака) вычислять по формуле:
, то допускаются границы погрешности результата измерения (без учета знака) вычислять по формуле:
 , (2.27)
, (2.27)
где К – коэффициент, зависящий от отношения случайной и неисключенной систематической погрешностей;
 – оценка суммарного среднего квадратического отклонения результата измерения.
– оценка суммарного среднего квадратического отклонения результата измерения.
 ; (2.28)
; (2.28)

. (2.29)
При симметричной доверительной вероятности результат измерения представляют в виде
 .
.
В нашем примере имеем
U = 12,415 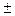 0,00704, Р = 0,9.
0,00704, Р = 0,9.
С учетом требований стандарта запишем результат измерения таким образом, чтобы наименьшие разряды (не более двух значащих цифр) числового значения результата измерения и численного показателя точности были бы одинаковы, т.е. U = 12.42 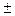 0,01, Р = 0,9.
0,01, Р = 0,9.
Не нашли, что искали? Воспользуйтесь поиском: