Погрешности совместных и совокупных измерений

Совместимыми называют проводимые одновременно измерения двух или нескольких разноименных величин для нахождения зависимости между ними, например, зависимости сопротивления от температуры.

Совокупными называют производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величины находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин или ряда других величин, функционально связанных с измеряемыми.

Для определения m искомых значений величин Y ₁; Y ₂;...; Y_m необходимо, чтобы число уравнений n было равным или больше числа неизвестных m. Так как решение системы уравнений относительно каждой из искомых величин Y ₁; Y ₂;...; Y_m представляет собой функцию, то результат измерения каждой из величин можно рассматривать как результат косвенного измерения. Дальнейшую обработку можно проводить по правилам обработки результатов наблюдений при косвенных измерениях. Если число различных совокупных измерений больше числа измеряемых величин, то отработку результатов измерения проводят с помощью метода наименьших квадратов (метод Лежандра).

Рассмотрим сущность метода наименьших квадратов на примере простой линейной зависимости вида y = a + bx, требуется найти параметры a и b так, чтобы теоретическая аппроксимирующая прямая обеспечила минимальное значение суммы квадратов отклонений экспериментальных значений y_i от теоретических y_i^`

^.

Для нашего случая имеем

.

Берем частные производные и приравниваем их к нулю:

и .

Получим систему двух линейных уравнений для определения параметров a и b:

;

.

(2.34)

Введем обозначения, разделив уравнения на

, , , ,

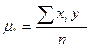преобразуем систему (2.34) к виду :

С помощью определителей решим эту систему и найдем параметры a и b:

; . (2.35)

Выражения (2.35) определяют значения параметров в зависимости от полученных в опыте значений.

Пример. Величины сжатия х_i стального бруса под действием нагрузки y_i приведены в табл. 2.13. Провести сглаживание экспериментальной зависимости от линейной зависимости, отвечающей закону Гука.

Таблица 2.13

Номер измерения
хi, мкм
yi, кг	51.33	78.00	144.30	263.60	375.20

Решение.

Пусть сглаживающая линейная зависимость имеет вид y = a + bx. Параметры a и b при сглаживании по методу наименьших квадратов вычисляют по формулам (2.35). Для их вычисления составим вспомогательную таблицу 2.14.

Таблица 2.14

Номер измерения
хi 2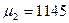
хi , yi	256.65

,

.

Окончательно получим y = 22.26 + 5,93* x.

На рис. 2.6 показан ход зависимости y от x

Не нашли, что искали? Воспользуйтесь поиском: