Вычисление статистических характеристик массивов

В практике массивами чаще всего представлены результаты каких–либо экспериментов или данные статистической отчетности предприятий. В таких случаях типовыми задачами обработки массивов являются вычисления их так называемых статистических характеристик. Важнейшими и наиболее употребительными из этих характеристик являются: среднее арифметическое, дисперсия и среднеквадратичное отклонение. Для массива x_i (i = 1..n) эти величины вычисляются соответственно по формулам:

Как следует из этих выражений, основной объем работы при определении этих величин, связан с вычислением двух сумм:

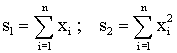
и поэтому фрагмент программы вычисления указанных статистических характеристик, обозначенных соответственно xsr, dis, sko, может быть следующим:

s1:=0; s2:=0;

for i:=1 to n do

Begin

s1:=s1+x[i];

s2:=s2+s2+sqr(x[i]);

end;

xsr:=s1/n; dis:=(s2/n–sqr(xsr))*n/(n–1); sko:=sqrt(dis);

writeln; write('xsr=',xsr,' dis=',dis,' sko=',sko);

Кроме среднего арифметического иногда используются еще три вида средних величин, вычисляемых по формулам:

среднее квадратическое (оно не равно среднеквадратическому отклонению)

;

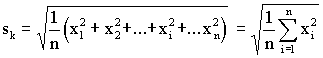среднее геометрическое

;

среднее гармоническое

.

Вычисление этих величин сводится в конечном итоге к вычислению соответствующих сумм и произведения и не представляет труда.

Не нашли, что искали? Воспользуйтесь поиском: