Создание новых массивов при решении задач

Часто при решении практических задач возникает необходимость создания нового массива из выборочных элементов исходного массива. Особенностью этого типа задач является то, что индексы элементов этих массивов не совпадают. Следовательно, в цикле должны изменяться два параметра и необходимо использовать прием организации цикла с несколькими одновременно изменяющимися параметрами. Обычно в блоке решения перед циклом начальные значения индексов новых массивов принимаются равными нулю. Далее в цикле по мере отбора элементов в новый массив вычисляется текущее значение этих индексов, которые и присваиваются соответствующим элементам. Смотри примеры 3, 4 и 5.

Операции с двумерными массивами (матрицами)

Двумерным называется массив, у которого размерность равна 2. Фактически он представляет собой таблицу состоящую из строк и столбцов. Двумерные массивы, у которых значения индексов одинаковые, т.е. число строк равно числу столбцов, называют квадратной матрицей. При работе с квадратными матрицами используются специальные математические понятия, значение которых рассмотрим на примере матрицы размерами 4х4 – B (4,4):

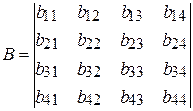
j = i – элемент находится на главной диагонали ();

j = n - i + 1 (n – размерность матрицы) – элемент находится на побочной диагонали ();

i < j – элемент находится над главной диагональю (, , , , , );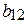

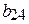i > j – элемент находится под главной диагональю (, , , , , ).

Транспонированной матрицей В (n, n) называется такая квадратная матрица, у которой столбцы соответствуют строкам исходной квадратной матрицы А (n, n):

Элементы главной диагонали у матриц А и В одни и те же. Следовательно операция транспонирования матрицы А сводится к перестановке строк матрицы.

Dim a() As Single

Dim b() As Single

n = 5

ReDim a(n, n): ReDim b(n, n)

For i = 1 To n

For j = 1 To n

a(i, j) = Cells (i, j)

b(j, i) = a(i, j) 'транспонирование матрицы

Next j

Next i

For i = 1 To n

For j = 1 To n

Cells (n + 1 + i, j) = b(i, j) 'вывод результата

Next j

Next i

Результат программы:

Не нашли, что искали? Воспользуйтесь поиском: