Порядок выполнения работы. 1. Получить у преподавателя индивидуальное задание и выполнить постановку задач: сформулировать условия

8. Оформить отчет о лабораторной работе в составе: постановка задачи, математическая модель, схема алгоритма, текст программы, контрольные примеры.

Варианты индивидуальных заданий

1. По введенным с клавиатуры значениям X, m вычислить S:

2. Вычислить предел последовательности { } при n® , где Y_n вычисляется по формуле …

Значения Y₀, Y₁ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n - Y_n-1ï<e.

1. По введенным с клавиатуры значениям X, m вычислить P:

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле Y_n= 0.2 + 0.1 sin(Y_n-1); n=1,2,3...

Значение Y₀ вводится с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. По введенным с клавиатуры значениям A, B, n, m и X вычислить S:

2. Вычислить предел последовательности {Y_n} при n® ,где Y_n вычисляется по формуле

Y_n=0.1 tg () + 0.3 tg (); n=3,4,5...

Значения Y₀, Y₁, Y₂ вводятся с клавиатуры. Вычисления прекращаются при выполнении условия ïY_n – Y_n-1ï<e.

1. По введенным с клавиатуры значениям A, B, n и X вычислить S:

2. Вычислить предел последовательности {Y_n} при n® ,где Y₀=0, а Y_n вычисляется по формуле

Значение Y₀ вводится с клавиатуры. Вычисления прекращаются при выполнении условия ïY_n – Y_n-1ï<e.

1. По введенным с клавиатуры значениям A, B, n, m и X вычислить S:

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле

Значения Y₀, Y₁ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. Вычислить сумму S значений функции Y=f(x):

; при

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле

Значения Y₀, Y₁ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. Вычислить сумму S значений функции Y=f(x):

; при

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле

Значения Y₀, Y₁, Y₂ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. По введенному с клавиатуры значению X вычислить S:

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле

Значения Y₀, Y₁ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. Для заданного с клавиатуры значения N найти

2. Вычислить предел последовательности {Y_n} при n® , где Y_n вычисляется по формуле

Значения Y₀, Y₁, Y₂ вводятся с клавиатуры. Вычисления прекратить при выполнении условия ïY_n – Y_n-1ï<e.

1. Для заданного с клавиатуры значения N найти

2. Последовательность функций Y_n = Y_n(x), где определяется следующим образом:

При заданном X найти предел последовательности, принимая за таковой значение Y_n, удовлетворяющее условию ïY_n – Y_n-1ï<e.

1. Найти сумму всех целых чисел, кратных 5, из отрезка [A,B].

2. Последовательность функций Y_n = Y_n(x), где X >0 определяется следующим образом:

При заданном Х найти предел последовательности, принимая за таковой значение Y_n, удовлетворяющее условию ïY_n – Y_n-1ï<e.

1. Найти сумму всех целых чисел, кратных 7, из отрезка [A,B].

2. Найти предел произведения для последовательности {Y_n}, пользуясь рекуррентной формулой

Вычисления закончить при выполнении условия .

1. Найти сумму всех целых чисел, дающих при делении на 5 в остатке 3, из отрезка [A,B].

2. Вычислить - корень k-ой степени из положительного числа A, пользуясь последовательным приближением

За корень принять такое , при котором |X_n – X_n-1| < ε

1. Найти сумму всех целых чисел, дающих при делении на 7 в остатке 4, из отрезка [A,B].

2. Для приближенного решения уравнения Кеплера X-q*sin(X)=m, 0<q<1

полагают

При заданном m найти решение уравнения Кеплера, принимая за него такое , при котором |X_n – X_n-1| < ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить если известны Y₀, Y₁, Y₂, а вычисляется по формуле

2. Вычислить предел последовательности {Y_n} при n ,где Y_n вычисляется по формуле:

Вычисления прекращаются при выполнении условия ïY_n – Y_n-1ï<e.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить Y_m, если известны Y₀, Y₁,Y₂, а Y_i вычисляется по формуле

,m

2. Найти предел последовательности с точностью ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить если известны Y₀, Y₁, Y₂, а Y_i вычисляется по формуле

,m

2. Найти предел последовательности 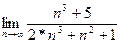с точностью ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить Y_m, если известны Y₀, Y₁, а Y_i вычисляется по формуле

,m

2. Найти сумму бесконечного ряда с точностью ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить Y_m, если известны Y₀,Y₁,Y₂, а Y_i вычисляется по формуле

Y_i= sin² (Y_i-1) + cos² (Y_i-3); i=3,4,5, …,m

2. Найти сумму бесконечного ряда с точностью ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить , если известны Y₀, Y₁, Y₂, а вычисляется по формуле

i=3,4,5,…,m

2. Найти сумму бесконечного ряда 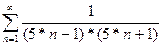с точностью ε.

1. Пользуясь рекуррентной формулой для заданного с клавиатуры m, вычислить при известных Y₀,Y₁, если Y_i вычисляется по формуле

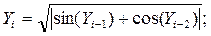i=2,3,4,…,m

2. Найти сумму бесконечного ряда с точностью ε.

1. Члены последовательностей {X_i} и {Y_i} вычисляются по двум рекуррентным формулам. Вычислить X₂₀,Y₂₀, если

2. Найти сумму бесконечного ряда с точностью ε.

Не нашли, что искали? Воспользуйтесь поиском: