Анықталмағандық қатынастар

Анықталмағандық принципі — физикалық жүйені сипаттайтын (қосымша физ. шамалар деп аталатын) шамалардың (мыс., координат және импульс) бір мезгілде дәл мәндер қабылдай алмайтындығын тұжырымдайтын кванттық теорияның іргелі қағидасы. 1927 ж. неміс физигі Вагнер Гейзенберг ашқан. Анықталмағандық принципі материя бөлшектерінің (электрондар, протондар, т.б.) корпускулалық-толқындық табиғаты болатындығын айқындайды. Сандық тұрғыдан Анықталмағандық принципі былай тұжырымдалады: егер — жүйенің инерция центріндегі координатының анықталмағандық мәні, ал импульсының осіне проекциясының анықталмағандық мәні болса, онда осы анықталмағандықтардың көбейтіндісі Планк тұрақтысынан () кем болмайды Макроскопиялық шамалармен салыстырғанда аз шама болғандықтан, бұл қатынас атомдық масштабтағы құбылыстарға қатысты ғана орындалады. Анықталмағандық принципі атом ішіндегі құбылыстардың заңдылықтарын түсіндіру және кванттық механика саласының қалыптасуы кезінде аса маңызды рөль атқарды. Егер және сәйкесінше координаттың және импульстың орташа квадраттық ауытқулары болса:

,

мұндағы 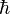— келтірілген Планк тұрақтысы. Анықталмағандық қатынасы - екі орайлас физикалык шамалар мәніндегі анықталмағандықтардың көбейтіндісі (мысалы, импульс пен координатаның, энергия мен уақыттың) Планк тұрақтысынан кіші болуы мүмкін емес дейтін тұжырым.^[1] Қозғалып келе жатқан, импульсі р бөлшекпен байланысқан де Бройль толқынының интенсивтігі бөлшектікеңістіктің берілген аумағынан табу ықтималдығын анықтайтыны өткен тақырыпта айтылды. Жазық монохромат толқын х осінің бойымен таралып жатсын. Онда бұл толқынға сәйкес бөлшектің импульсі р = р_х бірмәнді дәл анықталған. Бірақ жазық монохромат толқынның амплитудасы барлық жерде бірдей, сондықтан біз бөлшектің қай жерде екенін біле алмаймыз, яғни оныңкоординатасы анықталмаған. Бұл қиындықтан шығу үшін бөлшекті монохромат толқынмен емес, жиіліктері бір-біріне өте жақын бірнеше толқындардың қосындысымен, яғни ұзындығы Δх болатын толқындық пакет арқылы модельдеп көрейік. Толқындық пакеттің амплитудасы бөлшек орналасқан кеңістіктің кішкене аумағынан басқа жердің бәрінде нөлге тең, ал бөлшектің жылдамдығытолқындық пакеттің топтық жылдамдығына тең болсын. Енді біз бөлшектің координатасын қандай да бір Δх дәлдікпен анықтай аламыз, бірақ толқын ұзындығын λ=Δх/n (мұндағы n — Δх ұзындыққа сыятын толық периодтардың саны) дәл анықтай алмаймыз. Себебі толқындық пакеттің шекарасы дәл тағайындалмайды. Олай болса, λ=h/p болғандықтан, импульстің мәні де Δр_x шамасына анықталмайды. n неғұрлым үлкен болса, толқын ұзындығын, ол арқылы импульсті соғұрлым дәл анықтаймыз. Бірақ n өскен сайын координатаны анықтау дәлдігі төмендей береді, себебі толқындық пакеттің ұзындығы артады. Біз бұл жерде сәйкес оське қатысты координата мен импульстің проекциясын бір мезетте анықтау туралы айтып отырмыз.

Бірінің мәнінің анықталмағандығы екіншісін өлшеу дәлдігіне тәуелді шамалар жұбын (мысалы, х пен р_x) түйіндес шамалар деп атайды.

Не нашли, что искали? Воспользуйтесь поиском: