
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Биграммный шифр Плейфейра
Шифр Плейфейра, изобретенный в 1854 г., является наиболее известным биграммным шифром замены. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.
Можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса.
Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица:
| Б | А | Н | Д | Е | Р | О | Л |
| Ь | В | Г | Ж | И | Й | К | |
| М | П | С | Т | У | Ф | Х | Ц |
| Ч | Ш | Щ | Ы | Ъ | Э | Ю | Я |
Процедура шифрования включает следующие шаги:
1. Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
2. Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а. Если обе буквы биграммы открытого текста не попадают на одну строку или столбец - ОВ.
2б. Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в. Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.).
Зашифруем текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Разбиение этого текста на биграммы дает
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При расшифровании применяется обратный порядок действий.
1.9 Шифр "двойной квадрат" Уитстона
В 1854 г. англичанин Чарльз Уитстон разработал новый метод шифрования биграммами, который называют "двойным квадратом". Свое название этот шифр получил по аналогии с полибианским квадратом. В отличие от полибианского шифр "двойной квадрат" использует сразу две таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в шифре Плейфейра.
Рассмотрим процедуру шифрования этим шифром на примере. Пусть имеются две таблицы со случайно расположенными в них русскими алфавитами (рис.2). Перед шифрованием исходное сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую букву биграммы находят в левой таблице, а вторую букву – в правой таблице. Затем мысленно строят прямоугольник так, чтобы буквы биграммы лежали в его противоположных вершинах. Другие две вершины этого прямоугольника дают буквы биграммы шифртекста.
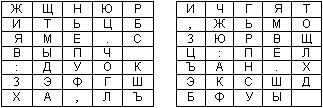
Рис. 2 – Две таблицы со случайно расположенными символами русского алфавита
Предположим, что шифруется биграмма исходного текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква Л находится в столбце 5 и строке 4 правой таблицы. Это означает, что прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5 правой таблицы. Следовательно, в биграмму шифртекста входят буква О, расположенная в столбце 5 и строке 2 правой таблицы, и буква В, расположенная в столбце 1 и строке 4 левой таблицы, т.е. получаем биграмму шифртекста 0В.
Если обе буквы биграммы сообщения лежат в одной строке, то и буквы шифртекста берут из этой же строки. Первую букву биграммы шифртекста берут из левой таблицы в столбце, соответствующем второй букве биграммы сообщения. Вторая же буква биграммы шифртекста берется из правой таблицы в столбце, соответствующем первой букве биграммы сообщения. Поэтому биграмма сообщения ТО превращается в биграмму шифртекста ЖБ. Аналогичным образом шифруются все биграммы сообщения:
Сообщение ПР ИЛ ЕТ АЮ _Ш ЕС ТО ГО
Шифртекст ПЕ 0В ЩН ФМ ЕШ РФ БЖ ДЦ
Шифрование методом "двойного квадрата" дает весьма устойчивый к вскрытию и простой в применении шифр. Взламывание шифртекста "двойного квадрата" требует больших усилий, при этом длина сообщения должна быть не менее тридцати строк.
Гаммирование
Под гаммированием понимают процесс наложения по определенному закону гаммы шифра на открытые данные. Гамма шифра – это псевдослучайная последовательность, выработанная по заданному алгоритму для зашифрования открытых данных и расшифрования зашифрованных данных.
Процесс зашифрования заключается в генерации гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым образом, например с использованием операции сложения по модулю 2.
Следует отметить, что перед зашифрованием открытые данные разбивают на блоки 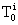 одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности блоков
одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности блоков 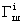 аналогичной длины.
аналогичной длины.
Уравнение зашифрования можно записать в виде
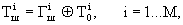
где 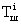 - i-й блок шифртекста;
- i-й блок шифртекста; 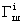 - i-й блок гаммы шифра;
- i-й блок гаммы шифра; 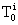 -i-й блок открытого текста; М - количество блоков открытого текста.
-i-й блок открытого текста; М - количество блоков открытого текста.
Процесс расшифрования сводится к повторной генерации гаммы шифра и наложению этой гаммы на зашифрованные данные. Уравнение расшифрования имеет вид
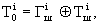
Получаемый этим методом шифртекст достаточно труден для раскрытия, поскольку теперь ключ является переменным. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого блока. Если период гаммы превышает длину всего шифруемого текста и злоумышленнику неизвестна никакая часть исходного текста, то такой шифр можно раскрыть только прямым перебором всех вариантов ключа. В этом случае криптостойкость шифра определяется длиной ключа.
Задание
1. Изучить алгоритм, заданный вариантом.
2. Построить математическую модель алгоритма.
3. Создать оконное приложение для реализации алгоритма
Варианты
1. Шифр Цезаря с ключом К=5
2. Шифр Цезаря с ключевым словом «БЕЗПЕКА»
3. Шифр Цезаря многоалфавитный
4. Шифр Гронсфельда з ключом 5263
5. Система шифрования Вижинера з ключевым словом «БЕЗПЕКА»
6. Полибианский квадрат
7. Полибианский квадрат с ключевым словом «БЕЗПЕКА»
8. Шифрующая таблица Трасмуса с ключевым словом «БЕЗПЕКА»
9. Шифр Цезаря с ключом К=-5
10. Шифр Цезаря с ключевым словом «ЗАХИСТ»
11. Шифр Цезаря многоалфавитный
12. Шифр Гронсфельда с ключом «ЗАХИСТ»
13. Система шифрования Вижинера з ключевым словом «ЗАХИСТ»
14. Полибианский квадрат с ключевым словом «ЗАХИСТ»
15. Шифрующая таблица Трасмуса с ключевым словом «ЗАХИСТ».
16. Шифрование методом Вернама.
Дополнительные варианты (повышенной сложности):
17. Шифр Уинстона
18. Аффинная система подстановок Цезаря
19. Шифр Плэйфеpа
20. Шифрование методом гаммирования.
Не нашли, что искали? Воспользуйтесь поиском: