ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Задания по физике для самостоятельной работы студентов

Дарибазарон Э.Ч., Санеев Э.Л., Шагдаров В.Б.

Редактор Т.Ю.Артюнина

Подготовлено в печать 2001 г. Формат 60´80 1/16

Усл.п.л. 3,72; уч.-изд.л. 3,2; Тираж 150 экз.

___________________________________________________

РИО ВСГТУ, Улан-Удэ, Ключевская, 40а

Отпечатано на ротапринте ВСГТУ, Улан-Удэ,

Ключевская, 42.

Ó Восточно-Сибирский государственный

технологический университет

Министерство образования РФ

ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

ЗАДАНИЯ ПО ФИЗИКЕ

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

РАЗДЕЛ: ”ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК"

Составители: Дарибазарон Э.Ч.,

Санеев Э.Л.,

Шагдаров В.Б.

Улан-Удэ 2002

ОСНОВНЫЕ ФОРМУЛЫ

Электростатика

1. Закон Кулона:

,

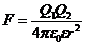где F - сила взаимодействия точечных зарядов Q₁ и Q₂:

r - расстояние между зарядами; e -диэлектрическая проницаемость, e₀ - 8,85×10^-12 Ф/м - электрическая постоянная.

2. Напряженность электрического поля и потенциал:

; ,

где П - потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).

3. Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:

;

4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):

;

где , j_i - напряженность и потенциал в данной точке поля, создаваемого i - м зарядом.

5. Напряженность и потенциал поля, создаваемого точечным зарядом:

; ,

где r- расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.

6. Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиуса R на расстоянии r от центра сферы:

а) если r < R, то Е = 0; ;

б) если r = R, то ; ;

в) если r > R, то ; ,

где Q - заряд сферы.

7. Линейная плотность заряда (заряд, приходящийся на единицу длину заряженного тела):

,

8. Поверхностная плотность заряда (заряд, приходящийся на единицу площади поверхности заряженного тела):

.

9. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длины d l с зарядом . Такой заряд можно рассматривать как точечный. Напряженность и потенциал (, dj) электрического поля, создаваемого зарядом dQ, определяется формулами:

; ,

где - радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.

Используя принцип суперпозиции электрических полей, находим интегрированием напряженность и, потенциал j поля, создаваемого распределенным зарядом:

;

.

Интегрирование ведется вдоль всей длины l заряженной линии (см. пример 6).

10. Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:

,

где r - расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.

11. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:

.

12. Связь потенциала с напряженностью:

а) в общем случае:

, или

б) в случае однородного поля:

;

в) в случае поля, обладающего центральной или осевой симметрией:

.

13. Электрический момент диполя:

,

где Q - заряд; l - плечо диполя (величина векторная, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

14. Работа сил поля по перемещению заряда Q из точки поля с потенциалом j₁, в точку с потенциалом j₂:

.

15. Электроемкость:

или ,

где j - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U - разность потенциалов пластин конденсатора.

16. Электроемкость уединенной проводящей сферы радиуса R:

.

17. Электроемкость плоского конденсатора:

,

где S - площадь пластины (одной) конденсатора; d - расстояние между пластинами.

18. Электроемкость батареи конденсаторов:

а) при последовательности соединении

;

б) при параллельном соединении

,

где N - число конденсаторов в батареи.

19. Энергия заряженного конденсаторов:

; ; .

Постоянный ток

20. Сила тока:

,

где Q - заряд, прошедший черех поперечное сечение проводника за время t.

21. Плотность тока:

,

где S - площадь поперечного сечения проводника.

22. Связь плотности тока со средней скоростью <v> направленного движения заряженных частиц:

,

где е - заряд частицы; n - концентрация заряженных частиц.

23. Закон Ома:

а) для участка цепи, не содержащего э.д.с.:

,

где j₁ - j₂ = U - разность потенциалов (напряжение) на концах участка цепи; r - сопротивление участка;

б) для участка цепи, содержащего э.д.с.:

,

где e - э.д.с. источника тока; r - полное сопротивление участка (сумма внешних и внутренних сопротивлений).

в) для замкнутой (полной) цепи

,

где r - внешнее сопротивление цепи, r_i - внутреннее сопротивление цепи.

24. Закон Кирхгофа:

а) первый закон

,

где - алгебраическая сумма сил токов, сходящих в узле;

б) второй закон

,

где - алгебраическая сумма произведений сил токов на сопротивления участков; - алгебраическая сумма э.д.с.

25. Сопротивление r и проводимость G проводника:

; ,

где r - сопротивление удельное; s - удельная проводимость; l -длина проводника; S - площадь поперечного сечения проводника.

26. Сопротивление системы проводников:

а) при последовательном соединении

;

б) при параллельном соединении

,

где r_i - сопротивление i-го проводника.

27. Работа тока:

; ; .

Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две - для участка, не содержащего э.д.с.

28. Мощность тока:

; ; .

29. Закон Джоуля-Ленца:

.

30. Закон Ома в дифференциальной форме:

,

где s - удельная проводимость, - напряженность электрического поля, - плотность тока.

31. Связь удельной проводимости с подвижностью в заряженных частиц (ионов):

?

где Q - заряд иона; n - концентрация ионов; в ⁺ ив^- - подвижность положительных и отрицательных ионов.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Три точечных заряда Q₁=Q₂=Q₃=1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Решение: Все три заряда, расположенные на вершинах треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например, Q₁, находился в равновесии. Заряд Q₁, будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис.1):

(1)

где , , - силы, с которыми соответственно действуют на заряд Q₁ заряды Q₂, Q₃, Q₄; - равнодействующая сил и .

Так как силы и направлены по одной прямой и в противоположные стороны, то векторное равенство (1) можно заменить скалярным равенством F - F₄ = 0, откуда

F₄ = F

Выразим в последнем равенстве F через F₂ и F₃ и учитывая, что F₃=F₂ получим .

Применяя закон Кулона и имея в виду, что Q₂=Q₃=Q₁, найдем

,

откуда

(2)

Из геометрических построений в равностороннем треугольнике следует, что

С учетом этого формула (2) примет вид

Подставим сюда числовое значение Q₁=1 нКл=10^-9 Кл получим

Следует отметить, что равновесие системы зарядов будет неустойчивым.

Пример 2. Тонкий стержень длиной l =20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии а =10 см от ближайшего конца находится точечный заряд Q₁= 40 нКл, который взаимодействует со стержнем с силой F=6 мкН. Определить плотность t заряда на стержне.

Решение. Сила взаимодействия заряженного стержня (F) с точечным зарядом Q₁ зависит от линейной плотности t заряда на стержне. Зная эту зависимость, можно определить t. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом.

dQ = t×dr. Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона,

Интегрируя это выражение в пределах от а до а +1, получим

,

Откуда интересующая нас линейная плотность заряда

.

Выразим все величины в единицах СИ:Q₁=40 нКл=4×10^-8 Кл, F=6 мкН=6×10^-6 Н, l =0,2 м, а =0,1 м, Ф/м.

Подставим числовые значения величин в полученную формулу и произведем вычисления:

Пример 3. Два точечных электрических заряда Q₁=1 нКл, Q₂= - 2 нКл находятся в воздухе на расстоянии d=10 см друг от друга. Определить напряженность и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда Q₁ на расстояние r₁=9 см и от заряда Q₂ на r₂=7 см.

Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей и полей, создаваемых каждым зарядом в отдельности: . Напряженность электрического поля, создаваемого в воздухе (e=1) зарядом Q₁, равна

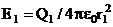(1),

зарядом Q₂ (2)

Вектор (рис.3) направлен по силовой линии от заряда Q₁, так как заряд Q₁ положителен: вектор: направлен также по силовой линии, но к заряду Q₂, так как заряд Q₂ отрицателен.

Абсолютное значение вектора найдем по теореме косинусов: (3)

где a - угол между векторами E₁ и E₂ который может быть найден на треугольнике со сторонами r₁, r₂ и d:

.

В данной случае во избежание громоздких записей удобно значение cosa вычислить отдельно:

Подставляя выражение E₁ из формулы (1) и E₂ из формулы (2) в равенство (3) и вынося общий множитель 1/4pe₀ за знак корня, получим

(4)

Подставим числовые значения величин в формулу (4) и произведем вычисления:

При вычислении Е знак заряда Q₂ опущен, так как знак заряда определяет направление вектора напряженности, а направление было учтено при его графическом изображении (рис.3).

В соответствии с принципом суперпозиции электрических полей потенциал j результирующего поля, создаваемого двумя зарядами Q₁ и Q₂ равен алгебраической сумме потенциалов, т.е.

j = j₁ + j₂ (5)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой

(6)

В нашем случае согласно формуле (5) и (6) получим

или

Подставим в это выражение числовые значения физических величин, получим

В.

Пример 4. Точечный заряд Q=25 нКл находится в поле, созданном прямым бесконечным цилиндром радиуса R=1 см, равномерно заряженным с поверхностной плотностью s=0,2 нКл/см². Определить силу F, действующую на заряд, если его расстояние от оси цилиндра r=10 см.

Решение. Численное значение силы F, действующей на точечный заряд Q находящийся в поле, определяется по формуле:

(1)

где Е - напряженность поля.

Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра

, (2)

где t - линейная плотность заряда.

Выразим линейную плотность t через поверхностную плотность s. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q двумя способами:

;

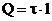
Приравняв правые части этих равенств и сократив на l, получим

С учетом этого формула (2) примет вид

(3)

Выпишем в единицах СИ числовые значения величин:

Q = 25 нКл = 2,5×10^-8 Кл, s = 0,2 нКл/см² = 2×10^-6 Кл/м², e₀ = 8,85×10^-12 Ф/м. Так как R и r входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах.

Подставим в (3) числовые значения величин:

мкН

Направление силы совпадает с направлением напряженности , последняя в силу симметрии (цилиндр бесконечно длинный) направлена перпендикулярно поверхности цилиндра.

Пример 5. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью V₁=10⁶ м/с, чтобы скорость его возросла в n=2 раза.

Решение. Ускоряющую разность потенциалов можно найти вычислив работу А сил электростатического поля. Эта работа определяется произведением заряда электрона е на разность потенциалов U:

А = е U, (1)

Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:

, (2)

где Т₁ и Т₂ - кинетические энергии электрона до и после прохождения ускоряющего поля; m - масса электрона; V₁ и V₂ - начальная и конечная скорости его.

Приравняв правые части равенств (1) и (2), получим

,

или ,

где n=V₂/V₁.

Отсюда искомая разность потенциалов

.

Подставим числовые значения физических величин и вычислим:

U = В = 8,53 В.

Пример 6. Конденсатор емкостью С₁=3 мкФ был заряжен до разности потенциалов U₁=40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емкостью С₂=5 мкФ. Какая энергия W’ расходуется на образование искры в момент присоединения второго конденсатора?

Решение. Энергия W’ израсходованная на образование искры

W’ = W₁ - W₂, (1)

где W₁ - энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора;

W₂ - энергия, которая имеет батарея, составленная из первого и второго конденсаторов.

Энергия заряженного конденсатора определяется по формуле

, (2)

где С - емкость конденсатора или батареи конденсаторов;

U - разность потенциалов на обкладках конденсаторов.

Выразив в формуле (1) энергии W₁ и W₂ по формуле (2) и принимая во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим

, (3)

где U₂ - разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что разряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U₂ следующим образом:

. (4)

Подставляя выражение (4) в формулу (3), получим

W’ = .

После простых преобразований найдем

.

В полученное выражение подставим числовые значения и вычислим W’:

Дж =1,5 мДж.

Пример 7. Сила тока в проводнике сопротивлением r = 20 Ом нарастает в течение времени Dt=2 с по линейному закону от J₀=0 до J=6 А (рис.4). Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ - за вторую, а также найти отношение Q₂/Q₁.

Решение. Закон Джоуля-Ленца в виде Q=J²rt справедлив для случая постоянного тока (J=const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

dQ=J²rdt (1)

Здесь сила тока J является некоторой функцией времени. В нашем случае

J=kt (2)

где k - коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т.е.

k= А/с

С учетом (2) формула () примет вид:

dQ = k² rt² dt (3)

Для определения теплоты, выделившейся за конечный промежуток времени Dt, выражение (3) надо проинтегрировать в пределах от t₁ до t₂.

.

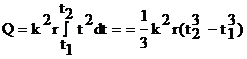При определении теплоты, выделившейся за первую секунду пределы интегрирования t₁=0, t₂=1 с и, следовательно:

Дж

При определении теплоты Q₂ пределы интегрирования t₁=1 с, t₂=2 с, тогда

Дж

Следовательно: Q₂/Q₁=420/60=7, т.е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.

Пример 8. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра (рис.5). В этой цепи r₁=100 Ом, r₂=50 Ом, r₃=20 Ом, э.д.с. элемента e₃=2 В. Гальванометр регистрирует ток J₃=50 мА, идущий в направлении, указанном стрелкой. Определить э.д.с. e₂ второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.

Решение. Выберем направления токов, как они показаны на рис.5 и условимся обходить контуры по часовой стрелке.

По первому закону Кирхгофа для узла F имеем

J₁ - J₂ - J₃ = 0 (1)

По второму закону Кирхгофа имеем для контура ABCDFA

-J₁r₁ - J₂r₂ = -e₁

или после умножения обеих частей равенства на -1

J₁r₁ + J₂r₂ = e₁ (2)

Соответственно для контура AFGHA

(3)

После подстановки числовых значений в формулы (1), (2), (3) получим:

Перенеся в этих уравнениях неизвестные величины в левые части, а неизвестные - в правые, получим следующую систему уравнений:

Эту систему с тремя неизвестными модно решить обычными приемами алгебры, но так как по условию задачи требуется определить только одно неизвестное e₂ из трех, то воспользуемся методом определителей.

Составим и вычислим определитель D системы:

Составим и вычислим определитель De₂:

Разделив определитель De₂ на определитель D, найдем числовое значение э.д.с. e₂:

В

КОНТРОЛЬНЫЕ ВОПРОСЫ

Не нашли, что искали? Воспользуйтесь поиском: