ТЕОРИЯ МЕТОДА И ОПИСАНИЕ УСТАНОВКИ. Рис.3. Лабораторный комплекс ЛКЭ – 1.

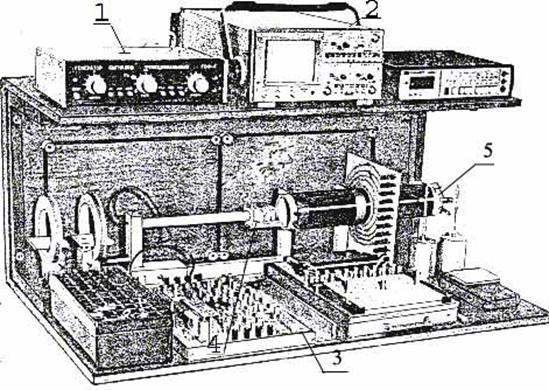
Рис.3. Лабораторный комплекс ЛКЭ – 1.

Магнитное поле соленоида измеряется индукционным методом с помощью ла­бораторного комплекса ЛКЭ-1 (рис.4), где 1 - генератор сигналов функциональный ГСФ-1; 2 - осцил­лограф тип С1-131/1; 3 - магазин сопротив­лений (датчиков тока); 4 - датчик эталонный на рейтере; 5 – длинный соленоид (два соленоида, соединенные последовательно).

Схема опытов по регистрации магнитного поля данным методом приведена на рис.4. На этом рисунке L1 – Контур, создающий магнитное поле. В данной работе в качестве L1 используются два соленоида, соединенные последовательно (поз. 5 на рис. 3). R1=1Ом - датчик тока. Для измерения магнитного поля используется L2 - индукционный эталонный (с заранее известными параметрами) датчик магнитного поля.

Индукционный датчик (рис. 5то катушка 1 из витков диаметром 20 мм (площадь витка =3,14 см 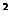), закрепленная на крон­штейне 2, установленном на рейтере 3, который может пе­ре­ме­щаться по рельсу 4. Под рельсом закреплена линейка 6, по кото­рой отсчитывается координата метки, нанесенной на рейтере. Катушка может поворачиваться вокруг вертикальной оси. Угол пово­рота от­считывается по шкале 5. Датчик регистрирует составляющую магнит­ного поля, парал­лельную оси катушки.

Если индукция магнитного поля зависит от времени, то в катушке возникает э.д.с., электромагнитной индукции:

,(4)

которая и измеряется для определения магнитного поля соленоида. В формуле (4) - поток магнитной индукции через площадь поперечного сечения датчика, 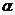- угол между вектором и нормалью к площадке .

Сигналы с датчиков поступают на два входа осциллографа. Измерения проводятся на частоте 100-500 Гц при пилообраз­ном токе в контуре L1 с размахом = 0,1 - 0,6 А. Для получения заданной формы тока генератор ГСФ – 1 работает в режиме генратора тока (кнопки S4 и S6 нажаты, см. рис. 7).

Примерная форма кривых на экране осциллографа приведена на рис.7. Эта форма соответствует закону электромагнитной индук­ции (4): э.д.с. индукции пропор­циональна производной магнитного потока по времени.

Из (4) следует

.

Проинтегрируем правую и левую части последнего уравнения.

,

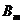где - период колебаний, - амплитуда магнитной индукции.

Учитывая, что , где - амплитуда напряжения на эталонном датчике, получим

.

Так как , где - размах напряжения на эталонном датчике, то

.

, где - частота колебаний.

Следовательно, экспериментальное значение амплитуды магнитной индукции в эталонном датчике при измерениях на прямоугольном сигнале в случае, когда :

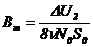. (5)

Расчетное значение индукции магнитного поля внутри длинного соленоида:

, (6)

где 160 мм - длина одного соленоида; - число витков в одном соленоиде; 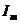- амплитудное значение тока в резисторе ; - амплитудное значение напряжения на резисторе (датчике тока); - размах напряжения на датчике тока.

Если измерения в опытах проводятся насинусоидальномсигнале (), то в этом случае в качестве источника сигнала годится как генератор тока, так и генератор напряжения, практически - любой достаточно мощный генератор гармонических сигналов.

В зависимости от измерительных приборов (вольтметр или осцил­лограф), измеряем:

- эфф. напряжение на датчике тока или его размах ;

- эфф. напряжение на эталонном датчике или его размах .

;

.

Экспериментальное значение амплитуды магнитной индукции в эталонном датчике при измерениях на синусоидальном сигнале в том случае, когда :

, (5*)

где .

Расчетное значение индукции магнитного поля внутри длинного соленоида при измерениях на синусоидальном сигнале:

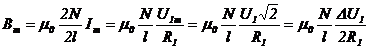, (6*)

где .

В дальнейшем, если измерения проводятся на прямоугольном сигнале, то все рассуждения ведутся относительно формул (5) и (6); если на синусоидальном – относительно формул (5*) и (6*).

Не нашли, что искали? Воспользуйтесь поиском: