Выполнение работы производится в строгом соот­ветствии с порядком проведения работы.

Результаты заносятся на отдельный лист, который в конце работы подписывается преподавателем. После чего результаты переносятся в подготовленные таблицы отче­та.

При обработке результатов измерений должны вы­полняться следующие требования:

- вычисления расчетных величин приводятся в отчете вследующей форме: выписывается сначала формула в об­щем виде, затем та же формула с подстановкой числен­ных значений (без наименований, в системе СИ) и затемответ. Промежуточные вычисления в отчете не приводят­ся.

- если одна и та же величина вычисляется несколько раз,то при повторных вычислениях можно не повторять об­щей формулы,

- если исходные данные и результаты вычислений зано­сятся в таблицу, содержащую большое число однородныхрезультатов, то достаточно привести в отчете только одинпример вычисления в указанной выше форме.

- вычисление относительной погрешности проводитсятакже как и вычисления расчетных величин - выписыва­ется формула в общем виде, затем та же формула с под­становкой численных значений (без наименований, всистеме СИ), численные значения каждого слагаемогоотносительной погрешности и полная погрешность ре­зультата.

При подстановке в формулу погрешностей данные можно округлять, сохраняя только две значащие цифры (окончательное усреднение с сохранением одной знача­щей цифры производится уже после вычислений абсо-

лютной и относительной погрешности). Если непосредст­венно вычислялась абсолютная погрешность результата, то отдельно указывается и величина относительной по­грешности.

Если в методическом указании требуется изобразить графически некоторую зависимость у = Г(х), то необходи­мо представить ее на миллиметровой бумаге, проводя построения с помощью чертежных принадлежностей. Ес­ли из графика получены какие-либо численные данные (например, наклон прямой), они указываются как на гра­фике, так и в тексте отчета.

ПРАВИЛА ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНЫМ РАБОТАМ

Оформление отчета должно содержать:

- номер лабораторной работы

- название лабораторной работы

- цель лабораторной работы

- краткий конспект теоретического введения

- описание установки

- результаты измерений.

-

В кратком конспекте теоретического введения необ­ходимо выписать определение изучаемого явления, фор­мулировки физических законов, отражающих суть изу­чаемого явления и их математическую запись, определе­ния входящих в них физических величин.

В описании установки привести обозначения, названия и размерности величин, используемых в расчетных формулах (здесь же приводятся значения используемых в ра­боте констант, взятых из описания или из справочных таблиц). Нарисовать чертеж, рисунок, блок-схему, элек­трическую или оптическую схемы, поясняющие идею применяемого метода измерений. Кратко сформулировать идею метода измерений.

ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЁТА ПО ЛАБОРАТОРНОЙ РАБОТЕ

ЛАБОРАТОРНАЯ РАБОТА 7

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА

Цель работы: экспериментальное определение момента инерции длинного стержня.

Приборы и принадлежности: длинный стержень, секундомер, линейка с мил­лиметровыми делениями, зажим с полкой.

РАСЧЕТНЫЕ ФОРМУЛЫ

1. Экспериментальное определение момента инерции.

,

где - момент инерции стержня относительно произвольной оси О,

- период колебаний физического маятника,

- время, за которое совершается 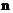полных колебаний,

- масса маятника,

- ускорение свободного падения,

- расстояние от центра тяжести С до оси колебаний О.

2. Теоретическое определение момента инерции.

Момент инерции относительно оси, проходящей через центр инерции перпен­дикулярно стержню:

,

где - длина стержня.

Момент инерции стержня относительно произвольной оси О:

(Теорема Штейнера).

РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ

Таблица

№ п.п.

, кг

, м

, м

, м

, м

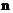, с

, с

, с

, с

, кгм2

, кгм2

, кгм2

Вычисляем момент инерции стержня относительно оси О (для и положения) по формулам:

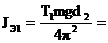
Вычисляем и по формулам:

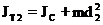
Вычисляем абсолютную и относительную погрешности опыта.

Абсолютная погрешность:

- -

Относительная погрешность:

Строим график зависимости .

1. Диск радиусом , находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 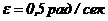. Найти тангенциальное , нормальное и полное ускорение точек на окружности диска в конце второй секунды после начала вращения.

2. Невесомый блок укреплен на конце стола (рис.). Гири 1 и 2 одинаковой массы соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол . Найти ускорение , с которым движутся гири, и силу натяжения нити. Трением в блоке пренебречь.

3. Тело брошено вертикально вверх со скоростью . Пренебрегая сопротивлением воздуха, определить, на какой высоте кинетическая энергия тела будет равна его потенциальной.

4. На барабан радиусом намотан шнур, к концу которого привя­зан груз массой Найти момент инерции барабана, если известно, что груз опускается с ускорением .

5. Физический маятник представляет собой тонкий однородный стержень длиною . Определить, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальной.

1. Свободно падающее тело в последнюю секунду движения проходит половину всего пути. С какой высоты падает тело и каково время его падения.

2. По наклонной плоскости с углом 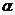наклона к горизонту, равным , скользит тело. Определить скорость тела вконце второй секунды от начала скольжения, если коэффициент трения .

3. С башни высотой горизонтально брошен камень со скоростью . Найти кинетическую и потенциальную энергию камня через время после начала движения. Масса камня .

4. Обруч и сплошной цилиндр, имеющие одинаковую массу , катятся без скольжения с одинаковой скоростью . Найти кинетическую энергию и этих тел

.

5. Найти возвращающую силу в момент и полную энергию мате­риальной точки, совершающей колебания по закону , где , . Масса материальной точки равна .

1. Поезд движется равнозамедленно, имея начальную скорость и ускорение . Через какое время и на каком расстоянии от начала пути торможения поезд остановится?

2. Тело массой падает вертикально с ускорением . Определить силу сопротивления при движении этого тела.

3. Тело массой движется со скоростью и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, найти количество теплоты , выделяющееся при ударе.

4. На однородный сплошной цилиндрический вал радиуса намо­тана легкая нить, к концу которой прикреплен груз массой . Груз, разматывая нить, опускается с ускорением . Определить: 1)момент инерции вала, 2) массу вала.

5. К пружине подвешен груз массой . Зная, что пружина под влиянием силы растягивается на , найти период вертикальных колебаний груза.

1.Точка движется по окружности радиусом с постоянным тангенциаль­ным ускорением . Через какое время после начала дви­жения нормальное ускорение будет: а) равно тангенциальному; б) вдвое больше тангенциального?

2. Две гири с массами и соединены нитью и перекинуты через невесомый блок. Найти ускорение , с которым движутся гири и силу натяже­ния нити . Трением в блоке пренебречь.

3. Конькобежец массой , стоя на коньках на льду, бросает в горизонтальном направлении камень массой со скоростью . На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лёд равен ?

4. Горизонтальная платформа массой и радиусом вращается с частотой . В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от до ? Считать платформу однородным диском.

5. Однородный диск радиусом колеблется около горизонтальной оси, проходящей на расстоянии от центра диска. Определить период колебаний диска

1. Тело брошено горизонтально со скоростью . Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через после начала движения.

2. Наклонная плоскость, образующая угол сплоскостью горизонта, имеет длину . Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время . Определить коэффициент трения 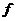тела о плоскость.

3. Человек массой , бегущий со скоростью , догоняет тележку массой , движущу­юся со скоростью и вскакивает на неё. С какой скоростью будет двигаться тележка?

4. Человек массой , стоящий на краю горизонтальной платформы массой , вращающейся по инерции вокруг неподвижной вертикальной оси с частотой

, переходит к её центру. Считая платформу круглым однородным диском, а человека - точечной массой, определить: с какой частотой , будет вращаться платформа.

5. Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз равна . Определить амплитуду второго колебания, если А.

ФИЗИКА

УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС

ТОПТ

УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС

Ответ: 18 мкПа • с.

12. В ультраразрежённом азоте, находящемся под давлением р - 1мПа и при температуре Т=300 К, движутся друг относительно друга две параллельные пластины со скоростью и - 1 м/с. Расстояние между пластинами не изменяется и много меньше средней длины свободного пробега молекул. Определить силу F внутреннего трения,

действующую на поверхность пластин площадью S = 1 м ". Ответ:" F = 0,89 мкН.

2.2. ОСНОВЫ ТЕРМОДИНАМИКИ

2.2.1. Тепловые процессы

Всякая система характеризуется параметрами Р, V, Т. Но не всегда эти параметры имеют определённые значения. Например, температура Т в различных точках системы различна. В этом случае системе нельзя приписать определённое значение Т. Такое состояние системы называют неравновесным. Процесс перехода системы из неравновесного состояния в равновесное называется процессом релаксации.

Равновесным называется такое состояние, при котором все параметры системы имеют определённые значения, остающиеся постоянными сколь угодно долго при неизменных условиях.

2.2.2. Внутренняя энергия спстелгы

Внутренняя энергия — энергия физической системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию теплового движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия частиц. В термодинамике рассматривается не само значение внутренней энергии, а её изменение при термодинамических процессах. Поэтому в термодинамике рассматривают те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах. Это:

1) кинетическая энергия поступательного движения молекул

2) кинетическая энергия вращательного движения молекул Е_вр;

3) кинетическая энергия колебательного движения атомов в

молекулах Е_к;

4) потенциальная энергия взаимодействия молекул между собой Епот:

U ~ Епост "

Епот.

В случае одноатомного идеального газа Е_вр = Е_к = Епот = 0. Тогда

22 В случае многоатомных молекул идеального газа Епот = 0:

. *

U = Епост + Евр + Ек = •- NkT,?

~.

м

ПОСТ 'Бр ' -'КОЛ '

Тогда

U =

М

RT.

2.2.3. Первое начало термодинамики

Обобщение многочисленных опытов дало возможность сделать вывод, что внутреннюю энергию можно изменить двумя путями:

1) за счёт передачи системе тепла;

2) за счёт работы, выполненной системой.

В случае теплоизолированной системы (адиабатически изолированной системы) передачи тепла нет и внутренняя энергия может быть изменена лтпнь за счёт работы, совершенной самой системой Д U = -ДА.

Знак минус означает, что работа, выполненная системой, совершается за счёт уменьшения внутренней энергии. Если изучаемая система представляет газ в цилиндре под поршнем площадью S, то при расширении газа поршень перемещается на расстояние dx и при этом газ совершает элементарную работу dA = Fdx = р • Sdx = pdV, "

где р = F/S — давление газа. Таким образом dU = - pdV.

Рассмотрим второй случай, когда механических' перемещений в системе нет. В этом случае объём V = const и работа не производится dA = 0. Тогда внутреннюю энергию можно изменить путём теплообмена. Если два тела или две системы с разными температурами привести в соприкосновение, то произойдёт передача тепла Д Q от более горячего тела к более холодному. Согласно закону

сохранения энергии тепло др, полученное системой идёт на увеличение внутренней энергии Д U - Д Q. Рассмотрев оба случая одновременно, можно записать.

113 Это и есть математическое выражение первого начала

термодинамики.

Чаще его записывают в виде Л Q = Д LJ+ Л А

и формулируют так: количество теплоты, сообщенное системе, расходуется на:

— изменение внутренней энергии системы;

— совершение системой работы против внешних сил.

Для исключения путаницы следует запомнить, что ДА в этом законе всегда представляет работу, совершаемую системой, a dQ > О если система получает тепло извне.

2.2.4, Теплоёмкость газов

Теплоёмкостью тела называется количество теплоты, " необходимое дта нагревания данного тела на 1 К с = dQ/dT.

Удельной теплоёмкостью называется количество теплоты, необходимое для нагревания единицы массы вещества на I К:

C = l/m-dQ/dT.

Мо.тярная теплоёмкость — количество теплоты, необходимое для нагревания i моля вещества на 1 К С_га = M/m-dQ/dT. (2.10)

Удельная теплоёмкость С связана с молярной С_т соотношением г - 1/ dQ/ _MdQ

^c'»-/v /dT--^f-^с'^м-

Единица удельной теплоёмкости [С] = Дж/кгК, единица молярной теплоёмкости [С_т] = Дж/(молъ К).

Различают теплоёмкости при постоянном объёме и постоянном давлении, если в процессе надевания вещества его объём или давление поддерживается постоянным.

Запишем выражение первого начала термодинамики с учётом того, что

d Q = — С_mdT (как это следует из (2.10)): М

^C_mdT = dU + pdV.

м

Если газ нагревается при постоянном объёме, то работа внешних сил dA = pdV равна нулю и сообщаемая газу извне теплота идёт только на увеличение его внутренней энергии:

— C_vdT = dU. (2.11)

С другой стороны, изменение внутренней энергии обусловлено изменением температуры газа

dU = — --RdT. (2.12)

М2 •

Сравнив (2.11) и (2.12) находим

c,-i«-

Если газ нагревается при постоянном давлении, то первое начало термодинамики, с учётом соотношения (2.12), можно записать:

^_CpdT = ^C_vdT+pdV. (2.13)

Используя уравнение Менделеева-Клайперона pV --— RT, найдём

М

m _,-„ работу газа прир = const: pdv - —Rdl.

М

Подставив полученное выражение в (2.13) получим

c_p=cv+r.

Это соотношение называется УГЖШШием__Майера. Оно

показывает, что Ср всегда больше Cv на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечиваегся увеличением объёма газа.

Используя выражение для Cv найдём Ср

C_p=iR ₊ R = i±iR.

Р? -,

При рассмотрении термодинамических процессов часто используют отношение С_р к C_v:

ср/ ₌i±2_ < +?-^ /C_v i " >~~^

' \ А.,/ /

Из полученных соотношений видно, что.мо.Арные теплоёмкости определяются липа числом степеней ев о бодал и не зависят от температуры. Это утверждение молекулярно-кннетической теории справедливо в довольно широком интервале температур лишь для одноатомиых газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоёмкости, зависит от температуры. Так пр_и__низких температурах колебательные и вращательные степени

свободы не.....проявляются"."При увеТпгчёнйй температуры начинают

проявляться"""вращательные степени свободы, а при дальнейшем ^сличений температуры и колебательные. 2.2.5. Применение первого начала

Не нашли, что искали? Воспользуйтесь поиском: