Работа №4. Определение емкости конденсатора

Цель работы: Изучение параметров магнитного поля, освоение методов измерения магнитных полей.

Краткая теория

Конденсатором называют систему, состоящую из двух изолированных проводников, пространство между которыми может быть заполнено диэлектриком. Эти проводники называют обкладками конденсатора. В зависимости от геометрии обкладок конденсаторы бывают плоские, цилиндрические или сферические (рис.1).

Рис.1

При зарядке конденсатора на его обкладках появляются равные по модулю и противоположные по знаку заряды. Заряд Q конденсатора (под зарядом конденсатора понимают заряд положительно заряженной его обкладки) оказывается пропорциональным напряжению U, созданному на его обкладках:

Q = CU,

причем коэффициент пропорциональности C не зависит от заряда и напряжения и является, таким образом, характеристикой конденсатора.

Физическую величину C, равную отношению заряда Q конденсатора к напряжению U на его обкладках

(1)

называют электроёмкостью (или просто ёмкостью) конденсатора. Ёмкость конденсатора зависит от формы и размеров его обкладок, расстоянию между ними, а также от диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками.

В качестве примера рассмотрим плоский конденсатор. Обкладками плоского конденсатора являются две одинаковые плоские проводящие пластины. Пусть S - площадь каждой из пластин, d - расстояние между ними, а E - диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами. Будем считать, что расстояние между пластинами много меньше их размеров, т.е.

Предположим, что в результате зарядки конденсатора на его обкладках появились заряды + Q и - Q (рис. 2)

Рис.2

Напряжённость электрического поля, создаваемого бесконечной плоскостью, равномерно заряженной по поверхности (т.к. ):

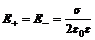
где – поверхностная плотность заряда.

Напряженность 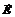результирующего поля находится согласно принципу суперпозиции:

Таким образом, для поля внутри конденсатора имеем:

Напряжение (разность потенциалов) на обкладках конденсатора при этом будет равным:

Для ёмкости плоского конденсатора окончательно получаем выражение:

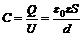(2)

Отметим, что при выводе формулы ёмкости плоского конденсатора мы считали поле в конденсаторе однородным. Однако однородность поля нарушается вблизи краёв конденсатора. Краевые эффекты вносят некоторую поправку к формуле (2), но её вычислением мы заниматься не будем.

Ёмкость конденсатора можно определить и экспериментально, чему и посвящена настоящая лабораторная работа.

Не нашли, что искали? Воспользуйтесь поиском: