Описание эксперимента. Как уже отмечалось, ёмкостью конденсатора называют отношение заряда конденсатора Qк напряжению U на его обкладках:

Как уже отмечалось, ёмкостью конденсатора называют отношение заряда конденсатора Q к напряжению U на его обкладках:

Таким образом, измеряя напряжение на конденсаторе и определяя его заряд, можно рассчитать ёмкость.

В настоящей лабораторной работе для определения ёмкости конденсатора собирается электрическая цепь, схематично показанная на рисунке 3.

Рис.3

Исследуемый конденсатор C заряжаем до напряжения источника 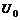посредством замыкания ключа K. Если ключ K снова разомкнуть, то конденсатор будет разряжаться через резистор R и микроамперметр.

Заряд, протекающий через микроамперметр в процессе разрядки конденсатора, будет равен и численно равен площади под графиком зависимости силы тока I в цепи от времени t (рис. 4)

Рис. 4

Таким образом, измеряя ток в цепи микроамперметром в разные моменты времени в процессе разрядки конденсатора и строя график зависимости силы тока от времени, можно найти заряд конденсатора Q как площадь под графиком I(t).

Если напряжение источника 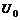неизвестно, то его нетрудно рассчитать по формуле

,

где - ток в цепи в начальный момент процесса разрядки конденсатора, а R - полное сопротивление цепи (внутренним сопротивлением микроамперметра мы пренебрегаем).

Предложенным способом можно лишь оценить ёмкость исследуемого конденсатора. Для более точного определения ёмкости рассмотрим следующий метод, использующий теоретическую зависимость силы тока от времени в процессе разрядки конденсатора. Рассмотрим состояния цепи в произвольный момент времени t (рис. 5). Пусть Q(t) - заряд конденсатора, а I(t) - ток в цепи в этот момент времени.

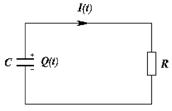
Рис. 5

Напряжение на конденсаторе , т.е.

(3)

Принимая во внимание закон сохранения заряда, получим соотношение, связывающее ток I с зарядом Q:

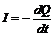(4)

В самом деле, пусть Q(t) - заряд конденсатора в произвольный момент времени t. Спустя малый промежуток времени dt с верхней обкладки конденсатора утечет заряд q=Idt и в момент времени t+dt на конденсаторе останется заряд

Таким образом, ,

что и требовалось показать.

Дифференцируя по времени уравнение (3) с учетом соотношения (4) получим дифференциальное уравнение для тока I:

Решение этого уравнения при начальном условии имеет вид:

(5)

Мы получили теоретическую зависимость тока в цепи I от времени t в процессе разрядки конденсатора. В настоящей лабораторной работе эта зависимость проверяется экспериментально. Для проверки зависимости (5) следует измерить значения силы тока в разные моменты времени и результаты измерений изобразить в виде точек на координатной плоскости XOY, где X = t, . Если экспериментальные точки в пределах точности измерений ложатся на прямую (рис. 6), то это подтверждает зависимость (5).

Рис. 6

Из соотношения (5) нетрудно получить выражение для ёмкости конденсатора

. (6)

Таким образом, измеряя значение силы тока I в начальный момент времени t = 0 и в момент времени t, зная сопротивление цепи R, можно рассчитать ёмкость C по формуле (6).

Погрешность в определении ёмкости, в соответствии с соотношением (6), может быть оценена по формуле:

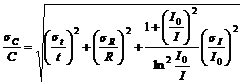(7)

При выводе формулы (7) полагалось, что .

Проанализируем при каких значениях тока I погрешность в определении ёмкости C будет минимальна.

Рассмотрим функцию y = f(x) вида

эта функция достигает минимального значения при .

Таким образом, надо измерить время t за которое значение силы тока в цепи после размыкания ключа уменьшается примерно в три раза и становится , и рассчитать ёмкость C по формуле (5). В этом случае погрешность σ_C будет минимальна и оценивается по формуле:

Не нашли, что искали? Воспользуйтесь поиском: