Таким образом, электрическая емкость плоского конденсатора

Пример 2. Сферический конденсатор. Сферический конденсатор состоит из двух концентрических металлических обкладок 1 и 2 сферической формы, радиусы которых соответственно равны R₁ и R₂ > R₁. Пусть + q- заряд первой обкладки, а – q- заряд второй обкладки. Напряженность поля в конденсаторе направлена радиально: E=E_r, причем

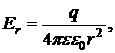
где e - относительная диэлектрическая проницаемость среды, заполняющей конденсатор. Так как

то разность потенциалов обкладок

Электрическая емкость сферического конденсатора

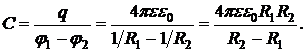
Пример 3. Цилиндрический конденсатор. Цилиндрический конденсатор состоит из двух тонкостенных металлических цилиндров высотой l и радиусами R₁ и R₂>R₁, вставленных друг в друга. Пусть заряд внутренней обкладки радиусом R₁ + q, а внешней, радиусом R₂ – q. Если l>>(R₁ и R₂), то, пренебрегая искажениями поля вблизи краев конденсатора, можно приближенно считать, что поле конденсатора такое же, как поле двух цилиндров бесконечной длины, заряженных с линейными плотностями зарядов t=q/l и -t. Внутри конденсатора поле создается только внутренней обкладкой. Так как s=t/(2pR₁)=q/(2pR₁l), следует что напряженность поля в диэлектрике с относительной диэлектрической проницаемостью e, заполняющем поле между обкладками конденсатора (R₁£r£R₂), равна E_r=q/(2pee₀ lr). (смотрите вывод в лабораторной работе № 1)

Так как

то разность потенциалов обкладок конденсатора

Не нашли, что искали? Воспользуйтесь поиском: