Электрическая емкость цилиндрического конденсатора

Эта формула выражает, в частности, емкость кабеля, который состоит из металлического провода, окруженного слоем изолятора и металлической броней.

Если напряжение на конденсаторе сделать слишком большим, то конденсатор «пробивается», т. е. между его обкладками возникает искра (внутри диэлектрика или по его поверхности) и конденсатор портится вследствие нарушения изоляции. Поэтому каждый конденсатор характеризуется не только своей емкостью, но еще и максимальным рабочим напряжением. Для того чтобы, располагая определенными конденсаторами, осуществить желаемую емкость при нужном рабочем напряжении, конденсаторы соединяют в батареи.

Рис 2.1

Соединение конденсаторов

На 2.1, а показано параллельное соединение конденсаторов. В этом случае общим для всех конденсаторов является напряжение U, и мы имеем

q₁=C₁U, q₂=C₂U,...

Суммарный заряд, находящийся на батарее, равен

Q=åq_i=UåC_i,

и поэтому емкость батареи

C=q/U=åC_i. (2.2)

Емкость батареи конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов. Так как в этом случае напряжение на каждом конденсаторе равно напряжению на батарее, то и допустимое рабочее напряжение батареи будет таким же, как и у одного конденсатора.

На рис. 2.1, б изображено последовательное соединение конденсаторов. В этом случае одинаков для всех конденсаторов заряд q,равный полному заряду батареи, и мы можем написать

U₁=q/C₁, U₂=q/C₂.

Напряжение же батареи будет равно сумме напряжений на отдельных конденсаторах, т. е.

.

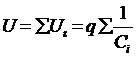Поэтому для емкости С всей батареи, находим

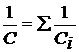. (2.3)

При последовательном соединение конденсаторов суммируются обратные значения емкостей. В этом случае напряжение на каждом конденсаторе будет меньше напряжения на батарее, и поэтому допустимое значение напряжения больше, чем у одного конденсатора.

На рис. 2.1, в показано смешанное соединение конденсаторов. Емкость такой батареи легко определить, пользуясь формулами (2.2) и (2.3).

При помощи гальванометра можно измерить не только силу тока, но и заряд, находящийся на каком-либо конденсаторе, что используется в данной работе. Рассмотрим, магнитоэлектрический гальванометр и будем считать, что трение при движении рамки настолько мало, что им можно пренебречь. Рамка является механической колебательной системой. Она имеет определенный момент инерции I и на нее действует сила упругости подвеса. Момент сил упругости подвеса М_п можно считать пропорциональным углу поворота рамки:

M_n= - fa,

где f зависит от устройств подвеса или спиральных пружин. Поэтому, будучи выведена из положения равновесия, рамка совершает механические крутильные колебания с периодом

.

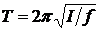Положим теперь, что мы замкнули на гальванометр какой-нибудь заряженный конденсатор. Конденсатор начнет разряжаться и в гальванометре возникнет кратковременный ток (импульс тока). Будем считать, что время импульса t мало по сравнению с периодом колебаний рамки: t<<T (баллистический режим). Тогда за время импульса рамка не успеет заметно сместиться, и все явления будет подобно явлению удара в механике. За время t на рамку подействует импульс момента силы, равный

,

где q -полный заряд, прошедший через гальванометр, μ - цена деления шкалы гальванометра в мкФ/дел. Поэтому рамка приобретает момент импульса

Iw₀= ,

(w₀- угловая скорость рамки) и кинетическую энергию

.

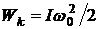После окончания импульса тока рамка начнет поворачиваться, и ее кинетическая энергия будет превращаться в потенциальную энергию закрученного подвеса:

W_n=fa²/2.

Поэтому, если a_m есть максимальный отброс, то

.

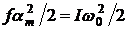Из этих уравнений находим

,

где b - постоянная прибора, называемая баллистическая постоянная. Мы видим, что, измеряя первый максимальный отброс гальванометра, можно определить полный заряд, прошедший через гальванометр.

Из зависимости q~a, исходя из определения емкости (2.1), следует, что

a ~ C. (2.4)

Выражение (2.4) можно записать в виде

C=a × μ.

Здесь С - емкость измеряемого конденсатора в мкФ, a - величина отброса стрелки гальванометра в делениях шкалы.

Построив график зависимости электроемкости от отброса стрелки гальванометра можно будет в дальнейшем, по известной электроемкости, сразу найти отброс стрелки гальванометра, и наоборот.

Описание установки