
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ КАТУШКИ
Цель работы: изучить распределение индукции магнитного поля на оси катушки, познакомиться с применением датчика Холла.
Оборудование: исследуемая катушка, блок питания, миллиамперметр, мультиметр, датчик Холла.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Магнитное поле – это форма материи, которая обнаруживает себя действием на магниты, на проводники с током и движущиеся заряды. Источником магнитного поля могут быть постоянные магниты, проводники с электрическим током и движущиеся электрические заряды, элементарные частицы, обладающие магнитным моментом.
Силовой характеристикой магнитного поля является вектор магнитной индукции В. По определению индукция равна отношению максимального момента сил к магнитному моменту стрелки или рамки с током:  , либо, согласно закону Ампера, как отношение максимальной силы, действующая на проводник, к силе тока и длине проводника:
, либо, согласно закону Ампера, как отношение максимальной силы, действующая на проводник, к силе тока и длине проводника:  .
.
Теоретический расчёт индукции магнитного поля проводников любой формы основан на применении принципа суперпозиции и закона Био – Савара – Лапласа для элемента проводника длиной dl, по которому течёт ток силой J:
 , (1)
, (1)
где m – относительная магнитная проницаемость среды; 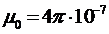 Гн/м – магнитная постоянная; r – радиус-вектор, проведенный из элемента dl проводника в точку наблюдения; a – угол между элементом dl и радиус-вектором r (рис.1).
Гн/м – магнитная постоянная; r – радиус-вектор, проведенный из элемента dl проводника в точку наблюдения; a – угол между элементом dl и радиус-вектором r (рис.1).

 Направление вектора dB можно определить правилом буравчика. Если вкручивать буравчик по току в проводнике, то направление перемещения конца ручки буравчика в точке наблюдения покажет направление вектора индукции магнитного поля (рис. 1).
Направление вектора dB можно определить правилом буравчика. Если вкручивать буравчик по току в проводнике, то направление перемещения конца ручки буравчика в точке наблюдения покажет направление вектора индукции магнитного поля (рис. 1).
Вывод формулы индукции магнитного поля катушки проведем в два этапа. Сначала определим, используя закон Био – Савара – Лапласа, индукцию магнитного поля одного витка радиуса R, с током J на его оси на расстоянии х от центра (рис. 2). Выберем малый элемент витка длины dl. Вектор dl направлен по касательной к витку, перпендикулярно радиус-вектору r, так что sin α = 1. Вектор индукции dВ элемента витка по правилу буравчика будет направлен перпендикулярно радиус-вектору r. Так же направлены векторы индукции других элементов витка, совпадая с образующими конуса. Результирующая векторов индукции будет совпадать с осью витка, и определяться интегралом  . Проинтегрировав и подставив
. Проинтегрировав и подставив  , получим формулу для индукции магнитного поля витка
, получим формулу для индукции магнитного поля витка
 . (2)
. (2)
На втором этапе определим распределение величины индукции магнитного поля вдоль оси катушки с равномерной обмоткой, по виткам которой течет ток силой J. Выделим на расстоянии х от середины катушки поперечными сечениями элементарный слой длиной dx с числом витков dN = ndx, где n – концентрация витков, то есть число витков на единицу длины катушки (рис. 3). В некоторой фиксированной точке А оси на расстоянии l от середины индукция выделенных витков определится формулой (2) при силе тока JdN = Jn dx. Результирующая индукция в точке А может быть определена суммированием по всем виткам катушки, то есть интегралом  .
.
 Интегрирование произведем по переменной – углу β. Из рисунка
Интегрирование произведем по переменной – углу β. Из рисунка  . Дифференцируя, получим формулу связи
. Дифференцируя, получим формулу связи  . Подставив его под знак интеграла
. Подставив его под знак интеграла 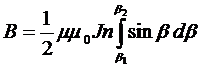 и проинтегрировав, получим
и проинтегрировав, получим
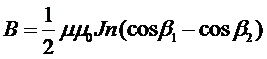 . (3)
. (3)
Здесь β 1 и β 2 – углы между радиус-векторами, проведенными из точки наблюдения А в крайние витки, и осью катушки. Через координату точки наблюдения они могут быть рассчитаны по формулам 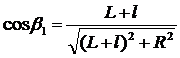 и
и 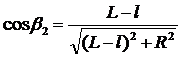 , где L– половина длины катушки.
, где L– половина длины катушки.
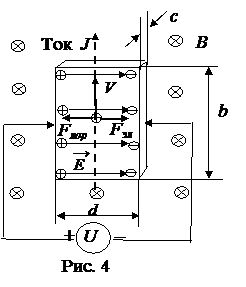
Экспериментальное изучение зависимости индукции магнитного поля на оси катушки в лабораторной работе производится с помощью датчика Холла. Эффект Холла состоит в появлении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле. Пусть по образцу в форме пластинки размерами d,b,c течет ток (рис.4). На движущиеся со скоростью дрейфа V заряды действует сила Лоренца  . Если носители заряда положительные, то, согласно правилу левой руки, под действием силы Лоренца они отклонятся на левую грань пластинки, если отрицательные, то на левую грань отклонятся отрицательные заряды (рис.4). В обоих случаях возникает поперечное электрическое поле, которое препятствует последующему отклонению зарядов.
. Если носители заряда положительные, то, согласно правилу левой руки, под действием силы Лоренца они отклонятся на левую грань пластинки, если отрицательные, то на левую грань отклонятся отрицательные заряды (рис.4). В обоих случаях возникает поперечное электрическое поле, которое препятствует последующему отклонению зарядов.
 Накопление зарядов на гранях прекратится и наступит равновесие, когда сила Лоренца будет уравновешена силой возникшего электрического поля
Накопление зарядов на гранях прекратится и наступит равновесие, когда сила Лоренца будет уравновешена силой возникшего электрического поля 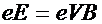 . ЭДС Холла будет равна
. ЭДС Холла будет равна  . Скорость дрейфа зарядов V можно определить по силе тока. Сила тока, по определению, равна заряду носителей тока в проводнике, прошедших через поперечное сечение проводника за единицу времени. Длина такого проводника численно равна скорости, а объем – Vdc. То есть
. Скорость дрейфа зарядов V можно определить по силе тока. Сила тока, по определению, равна заряду носителей тока в проводнике, прошедших через поперечное сечение проводника за единицу времени. Длина такого проводника численно равна скорости, а объем – Vdc. То есть  . Здесь nq,e – концентрация и заряд носителей. Подставив скорость в формулу ЭДС Холла, получим
. Здесь nq,e – концентрация и заряд носителей. Подставив скорость в формулу ЭДС Холла, получим 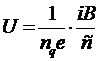 . Отсюда индукция измеряемого магнитного поля может быть определена по формуле
. Отсюда индукция измеряемого магнитного поля может быть определена по формуле
 , (4)
, (4)
где C – постоянная датчика.
Лабораторная установка состоит из блока питания постоянного тока, к которому подсоединяется модуль, в котором находится исследуемая катушка. Датчик Холла перемещается по оси катушки, его координата определяется по шкале линейки. ЭДС Холла измеряется мультиметром. Модуль и блок питания соединяются кабелем.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Проверить подключение мультиметра к гнездам «РА» модуля. Установить щуп датчика Холла в середину катушки. Включить предел измерения мультиметра 200 мВ. Убедиться, что ЭДС Холла близка к нулю.
2. Включить блок питания в сеть 220 В. Установить регулятором (5–24 В) силу тока J в катушке в интервале 1,0–3,0 А. Записать в табл. 1. Записать в табл. 1 параметры катушки и постоянную С.
Таблица 1
| Постоянная С, Тл/мВ | |
| Половина длины L, см | 8,8 |
| Радиус катушки R, см | 6,7 |
| Концентрация n 1/м3 | 13,1∙103 |
| Сила тока, J А |
3. Измерить ЭДС Холла, смещая датчик в возможном интервале перемещения через каждые 2 см. Записать расстояния и ЭДС в табл.2.
Выключить приборы
| х, см | ||||||||||||
| U, мВ | ||||||||||||
| В мТл |
Таблица 2
4. Произвести расчеты. Определить по формуле (4) индукцию магнитного поля в точках наблюдения. Записать в табл. 2.
5. Построить график зависимости индукции от расстояния х. Размер графика не менее половины страницы. Около точек провести плавную линию так, чтобы отклонение точек было минимальным.
6. Определить теоретическое значение индукции в центре катушки по формуле:  . Сравнить с экспериментальным значением В 0 в середине катушки. Сделать выводы.
. Сравнить с экспериментальным значением В 0 в середине катушки. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение магнитного поля и вектора индукции.
2. Запишите и сформулируйте закон Био–Савара–Лапласа, сформулируйте правило буравчика и приведите пример.
3. Выведите формулу индукции магнитного поля на оси витка.
4. Запишите формулу индукции магнитного поля катушки с током. Изобразите график зависимости индукции от расстояния.
5. Объясните причину возникновения эффекта Холла.
6. Выведите формулу для ЭДС Холла.
Работа 26 б
Не нашли, что искали? Воспользуйтесь поиском: