Проведение эксперимента. Определение удельного заряда электрона при помощи вакуумного диода осуществляется при использовании электрической схемы

Определение удельного заряда электрона при помощи вакуумного диода осуществляется при использовании электрической схемы, приведенной на рисунке 4. Для выполнения необходимых измерений необходимо установить сменную плату в универсальный лабораторный стенд и при помощи соединительный проводов и гнезд «3», «4», «5» подсоединить к схеме вольтметр. Включив приборы в сеть, дать им прогреться несколько минут.

Измерение анодного напряжения выполняется с помощью вольтметра. Для измерения напряжения вольтметр подключается между точками «3» и «5».

Анодный ток в цепи лампы определяется по падению напряжения на измерительном сопротивлении , которое снимают с точек «4» и «5». Величина анодного тока в цепи вычисляется делением напряжения на измерительном сопротивлении на величину сопротивления. Величина сопротивления указана на сменной плате.

Напряжение между анодом и катодом вычисляется как разность между напряжением на аноде и напряжением на измерительном сопротивлении, т.е. .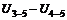

Измерение сопротивления выполняется омметром. Падение напряжения на сопротивлении измеряется вольтметром. Для измерения необходимо отключить питание стенда и при помощи соединительных проводов подключить омметр к точкам «4» и «5». Измерение напряжения на осуществляется при подключении вольтметра к этим же точкам.

Задание

Упражнение 1. Снять зависимость тока диода от анодного напряжения . Зависимость 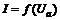представить графически и сравнить с теоретической зависимостью, для чего построить график зависимости квадрата анодного тока от куба напряжения между анодом и катодом диода.

Упражнение 2. Вычислить величину удельного заряда электрона на основании уравнения Богуславского–Ленгмюра по формуле (10) и подсчитать ошибку вычисления.

Контрольные вопросы

1. Что называется электровакуумными приборами? Типы электровакуумных приборов.

2. В чем заключается явление термоэлектронной эмиссии? Как определяется работа выхода электрона из металла?

3. Электровакуумный диод: схема, устройство и принцип работы («выпрямление» переменного тока).

4. Роль объемного пространственного заряда в работе диода.

5. Вольт-амперная характеристика вакуумного диода.

6. Режим насыщения анодного тока (когда достигается)?

7. Вывод формулы Богуславского–Ленгмюра.

8. Как можно определить удельный заряд электрона (методика определения).

9. Принцип работы транзистора Т в схеме эксперимента.

10. Объяснить принцип работы экспериментальной схемы.

11. Как измеряется анодный ток ?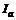

12. Как измеряется анодное напряжение ?

13. Методика расчета ошибки вычисления удельного заряда.

14. На каком участке вольт-амперной характеристики можно использовать формулу Богуславского–Ленгмюра? Почему?

ПРИЛОЖЕНИЕ 1

Закон степени 3/2

Для диода, работающего в режиме объемного заряда, анодный ток и анодное напряжение связаны нелинейной зависимостью, которая выражается законом трех вторых.

Рассмотрим зависимость силы тока, протекающего в вакууме между электродами, от приложенной разности потенциалов. Электроды будем считать плоскими, а ось 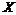направим нормально поверхности электродов. Потенциал катода примем за нуль 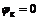, а потенциал анода обозначим 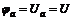(рисунок 1П1).

Допустим, что площади пластин катода и анода достаточно велики и при расчете плотности тока вблизи линии, соединяющей центры электродов, можно пренебречь изменением величин в направлениях, перпендикулярных этой линии, считая все величины зависящими только от координаты .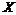

Уравнение Пуассона для потенциала имеет вид:

, (1П1)

где 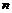– концентрация электронов.

Закон сохранения энергии для электронов, движущихся между анодом и катодом, запишется как:

, (2П1)

где 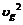– скорость движения электронов в точке с потенциалом .

Объемная плотность тока в этой точке:

. (3П1)

Все величины в правой части (3П1) являются положительными. Вычислив из уравнения (2П1) скорость , и подставив в уравнение (3П1), находим:

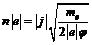. (4П1)

С учетом уравнения (4П1) уравнение Пуассона преобразуется к виду:

, (5П1)

где 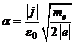– постоянная.

Умножая обе части уравнения (5П1) на 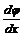, получаем:

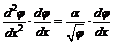. (6П1)

Учитывая, что:

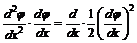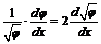; , (7П1)

уравнение (6П1) запишется в виде:

. (8П1)

Теперь можно проинтегрировать обе части полученного уравнения (8П1) по 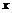в пределах от 0 до того значения 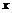, при котором потенциал равен . Тогда:

, (9П1)

где учтено, что .

Выше было показано, что напряженность поля на катоде равняется нулю, а, следовательно, и . Поэтому получаем:

(10П1)

или

. (11П1)

Интегрируя обе части уравнения (11П1) в пределах от 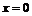, 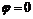до , 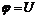получаем:

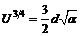. (12П1)

Возводя обе части в квадрат и учитывая, что: 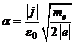, получаем:

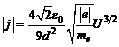(13П1)

или

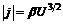, (14П1)

где .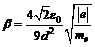

Учитывая, что плотность тока есть:

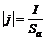, (15П1)

где 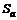– действующая площадь анода, получим зависимость силы тока, протекающего в вакууме между электродами, от приложенной разности потенциалов:

. (16П1)

Расчет аналогичной задачи для коаксиальных цилиндрических электродов, для концентрических сферических электродов приводит к такому же виду зависимости объемной плотности тока от разности потенциалов в степени три вторых. В случае коаксиальных сферических электродов выражение, называемое «законом 3/2» или уравнением Богуславского–Ленгмюра имеет вид:

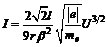. (17П1)

где 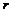– радиус анода, 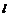– длина катода, 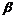– коэффициент, зависящий от отношения радиусов анода и катода.

Теоретическое рассмотрение вопроса о зависимости анодного тока от величины анодного напряжения в вакуумном диоде было проведено при следующих допущениях:

1) начальные скорости электронов, эмитируемых катодом, настолько малы, что можно считать их равными нулю;

2) анодный ток далек от насыщения;

3) объемный заряд создает такое распределение потенциала, что непосредственно у поверхности катода напряженность электрического поля равна нулю.

ЛАБОРАТОРНАЯ РАБОТА № 4

ИЗУЧЕНИЕ РЕЛЕКСАЦИОННЫХ ПРОЦЕССОВ В RC-ЦЕПИ

Цель работы: изучение зависимости тока и напряжения от времени в цепях, содержащих RC-элементы.

Приборы: универсальный лабораторный стенд, осциллограф, омметр, сменная плата, соединительные провода со штекерами.

Не нашли, что искали? Воспользуйтесь поиском: