Часть I. Методы расчета переходных процессов в линейных электрических

Цепях

I. Работа под руководством преподавателя 20 минут

Знакомство с расчетом переходных процессов при помощи

MathCAD.

II. Самостоятельная работа 60 минут

Часть II. Методы расчета мощности напряжения и тока в электрических цепях с синусоидальным и несинусоидальным периодическим электрическим током.

I. Работа под руководством преподавателя 20 минут

Знакомство с расчетом токов напряжений и мощности MathCAD в цепях с синусоидальными и несинусоидальным периодическим током.

II. Самостоятельная работа 60 минут

ЗАПУСК ПРОГРАММЫ:

Предполагается, что требуемые программы уже инсталлированы на диске.

Часть I. Методы расчета переходных процессов в линейных электрических

цепях

I. Знакомство с расчетом переходных процессов при помощи MathCAD

Рекомендуемое время

Минут

Переходные процессы могут быть легко рассчитаны при помощи преобразования Лапласа. С другой стороны при помощи MathCad легко найти обратное преобразование Лапласа и получить явную математическую формулу для зависимостей токов и напряжений переходных процессов.

1.1. Рассмотрим пример:

Необходимо рассчитать переходный процесс в следующей электрической цепи. При помощи MathCad построить график зависимости тока протекающего через индуктивность.

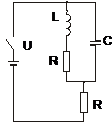1. Введем переменные u(s)- преобразование Лапласа напряжения на емкости, i(s)- Преобразование Лапласа тока, проходящего через индуктивность. Так как напряжение на емкости равно сумме падений напряжения на сопротивлении 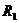и на индуктивности имеем:

(1)

С другой стороны, поскольку ток через емкость равен производной от ее напряжения, умноженный на величину С, а ток, проходящий через R равен сумме токов, проходящих через емкость и индуктивность имеем следующее выражение для преобразования Лапласа тока, проходящего через R

Так как напряжение источника питания равно сумме падений напряжений на сопротивлении R и емкости имеем:

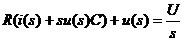; (2)

Решая систему уравнений (1) и (2) имеем:

(3)

2. В окно программы MathCad, вводим значения параметров цепи и напряжения.

Для получения математической формулы обратного преобразования Лапласа с помощью MathCAD выражение (3) необходимо упростить. Произведем замену переменных

Тогда искомое выражение примет вид:

3. Устанавливаем курсор на переменной s и выбираем опцию

Символика/Трансформация/Инверсия_Лапласа, получаем следующее аналитическое выражение для тока:

Выражение получилось очень длинным, для того чтобы поместиться на экране.

4. Копируем выражение в буфер обмена и набираем I(t):=. После этого правую часть копируем из буфера обмена.

5. Строим график переходного процесса.

Не нашли, что искали? Воспользуйтесь поиском: