ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
II. Самостоятельная работа. Рассчитайте переходные процессы для следующих электрических схем.
Рекомендуемое время
Минут
Задание:
Рассчитайте переходные процессы для следующих электрических схем.
1 Вариант 2 Вариант 3 Вариант 4 Вариант
5 Вариант
| № | U | R | R1 | R2 | L | L1 | L2 | C | C1 | C2 | Рассчитываемый параметр процесса |
| 7.2 | 6.7 | 1.8 | - | 5.9 | 8.7 | 5.3 | - | Ток через сопротивление R | |||
| 5.6 | 6.5 | 7.6 | - | - | - | - | 1.7 | 2.8 | Напряжение на С1 | ||
| 4.7 | 7.8 | 1.5 | 8.1 | - | - | - | - | Ток через L | |||
| - | 6.4 | 8.8 | 7.0 | 2.8 | - | - | - | Ток через L | |||
| - | 6.7 | 7.8 | - | - | - | 0.2 | - | - | Ток через R2 |
Часть II. Методы расчета мощности напряжения и тока в электрических
цепях с синусоидальным и несинусоидальным периодическим
электрическим током.
I. Знакомство с расчетом токов напряжений и мощности MathCAD в цепях с синусоидальным и несинусоидальным периодическим током.
Рекомендуемое время
Минут
Любая синусоидальная функция может быть представлена в виде 
где A – комплексная амплитуда. Для расчета токов и напряжений цепи при синусоидальном токе используют комплексные амплитуды. Расчет цепи становится аналогичным расчету цепи с постоянным током, только реактивное сопротивление емкости и индуктивности полагают равными 
и 
соответственно. При расчете цепи с периодическим несинусоидальным током токи и напряжения разлагаются в ряды Фурье и происходит расчет комплексных амплитуд для каждой гармонической составляющей. В приведенном ниже примере мы ограничимся расчетом периодического тока, так как синусоидальный ток представляет собой простейший частный случай периодического.
1.1. Рассмотрим пример:
 |
Дана следующая электрическая цепь
Напряжение источника питания периодично и разлагается на четыре гармонические составляющие. Требуется рассчитать ток, проходящий через индуктивность и напряжение на сопротивлении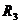 
, a также потребляемую цепью мощность.
Расчет цепи произведем методом контурных токов, которые изображены на рисунке. Введем обозначения 
и 
Тогда уравнения контурных токов имеют вид:
Или в векторно-матричном виде:
где 
Очевидно, что решение этого уравнения имеет вид
Данное уравнение надо решить для каждой гармонической составляющей. Осуществим это для каждой гармонической составляющей при помощи MathCAD. В результате имеем следующий код на MathCad.
Строим графики для напряжения питания, проходящего через индуктивность тока и падения напряжения на сопротивлении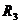
Потребляемая мощность при периодическом токе равна сумме потребляемых мощностей каждой гармонической составляющей. В свою очередь, потребляемая мощность гармонической составляющей равна 
где 
- величина, комплексно сопряженная комплексной амплитуде напряжения источника питания, а 
- комплексная амплитуда тока проходящего. В результате вычисления при помощи MathCad имеем:
Не нашли, что искали? Воспользуйтесь поиском: