ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теорема о циркуляции вектора магнитной индукции. Поле соленоида и тороида
В третьей лекции было показано, что для электростатического поля 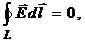
|
|
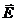 вдоль замкнутого контура L равна нулю. Можно показать, что циркуляция вектора
вдоль замкнутого контура L равна нулю. Можно показать, что циркуляция вектора 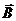 вдоль замкнутого контура L равна алгебраической сумме токов, охватываемых контуром, умноженной на
вдоль замкнутого контура L равна алгебраической сумме токов, охватываемых контуром, умноженной на 
 0, т. е.
0, т. е.
|
|

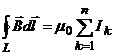 (1)
(1)



|
|




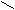
|
 . Токи, текущие в обратном
. Токи, текущие в обратном
направлении, будут считаться отрицательными. Для рис. 1, это будут токи, текущие на нас и обозначенные кружком с точкой в центре кружка.
Поскольку 
 , то магнитное поле не является потенциальным, оно называется
, то магнитное поле не является потенциальным, оно называется
вихревым или соленоидальным.
Теорему о циркуляции вектора  (1) называют также законом полного тока для магнитного поля в вакууме.
(1) называют также законом полного тока для магнитного поля в вакууме.
Применим теорему о циркуляции (1)для вычисления индукции магнитного поля соленоида и тороида.
Поле соленоида
|

 Соленоидом, (см. рис. 2), называется цилиндрическая катушка, на которую вплотную намотано большое число витков провода. Пусть N - число витков вдоль длины соленоида l, тогда
Соленоидом, (см. рис. 2), называется цилиндрическая катушка, на которую вплотную намотано большое число витков провода. Пусть N - число витков вдоль длины соленоида l, тогда 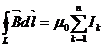 , где L – контур 12341
, где L – контур 12341

 или
или  .
.
Интегралы на участках 1-2, 3- 4 равны нулю, т.к. 
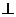
 и
и  = Bdl cos π /2 =0;
= Bdl cos π /2 =0;
интеграл на участке 4-1 равен нулю, т.к. вне соленоида индукция  равна нулю. Поэтому
равна нулю. Поэтому 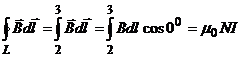 , отсюда B=
, отсюда B=  , (2)
, (2)
где n = N / l - число витков, приходящееся на единицу длины соленоида. Поле соленоида однородно.
Поле тороида
Тороид (см.рис.3), представляет тонкий провод, плотно навитый на каркас, имеющий форму тора. Для него 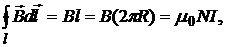
где R - радиус средней линии тора, отсюда B =  (3)
(3)
 Поле тороида неоднородно: оно уменьшается с увеличением r. Поле вне тороида равно нулю.
Поле тороида неоднородно: оно уменьшается с увеличением r. Поле вне тороида равно нулю.
Не нашли, что искали? Воспользуйтесь поиском: