ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. ПОТОК ЭНЕРГИИ.

Рассмотрим замкнутый объем, в котором электромагнитное поле возбуждается переменными токами с объемной плотностью .

По закону Джоуля-Ленца в дифференциальной форме: .

Найдем количество теплоты, выделяющееся в единицу времени в этом объеме: .

Используем, что .

Тогда: .

По теореме Гаусса: .

Слагаемые во втором интеграле можно представить в виде:

так как .

Аналогично можно представить: .

Тогда: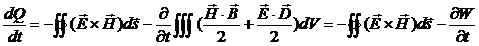

Подинтегральное векторное произведение напряженностей электрического и магнитного полей также представляет собой вектор 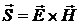, направленный по скорости распространения электромагнитной волны и равный по величине в любой момент времени: . При выводе этого соотношения использовано понятие объемной плотности энергии магнитного поля, которая, как показано Максвеллом, равна половине объемной плотности энергии электромагнитного поля.

Соответственно, для характеристики переноса энергии электромагнитной волной, вводится вектор Умова-Пойтинга , - плотность потока электромагнитной энергии через поверхность, ограничивающую рассматриваемый объем. Таким образом можно рассчитать поток энергии, проходящей через поверхность, ограничивающую данный объем: .

Выражение: представляет собой закон сохранения энергии электромагнитного поля, так как показывает, что изменение энергии электромагнитного поля в объеме определяется тепловой мощностью и потоком энергии через поверхность, ограничивающую объеме.

Если тепловых потерь нет, то или , т.е. вектор Умова-Пойтинга определяется энергией, проходящей в единицу времени через единичную поверхность, перпендикулярную направлению распространения волны. Полную энергию поля в рассматриваемом объеме можно, следовательно, рассчитать по формуле: .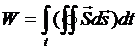

РИС.190 РИС.191 РИС.192

Не нашли, что искали? Воспользуйтесь поиском: