Теоретические сведения. Рассмотрим контур, состоящий из последовательно соединённых катушек индуктивности L, конденсатора С и сопротивления R (рис

Рассмотрим контур, состоящий из последовательно соединённых катушек индуктивности L, конденсатора С и сопротивления R (рис. 1).

Согласно второму правилу Кирхгофа:

U_C + U_R = ε_L ;

.

Учитывая, что

и ,

найдём

. (1)

Введём обозначения:

, , (2)

где d – коэффициент затухания, – собственная частота контура.

С учётом выражений (2) уравнение (1) примет вид

. (3)

Уравнениями вида (3) описывается обширный класс колебательных систем как электрических, так и механических. При условии, что затухание системы мало (d < w₀), решение уравнения (3) имеет следующий вид:

. (4)

Как видно из (4), величина заряда на обкладках конденсатора изменяется по закону затухающих колебаний. Учитывая, что и , зависимость напряжения и тока в контуре от времени определяются следующим образом:

, (5)

. (6)

График изменения напряжения изображён на рис 2. Амплитуда колебаний экспоненциально убывает. Коэффициент затухания d характеризует быстроту затухания за 1 сек.

Частота затухающих колебаний

. (7)

При d ¹ 0 напряжение, также как заряд и ток, не является вполне периодической функцией времени, т. к.

.

Говорить о периоде этой функции можно только в том смысле, что она принимает амплитудные значения через равные промежутки времени. Этот период называется условным и определяется выражением:

. (8)

Свойства колебательной системы характеризуют, указывая логарифмический коэффициент затухания D и добротность Q. Введём эти понятия. Возьмём отношение амплитуд двух последующих колебаний напряжения

.

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания

. (9)

Логарифмический декремент затухания, равный натуральному логарифму отношения амплитуд, отстоящих друг от друга на период, характеризует быстроту затухания колебаний за период. Для колебательного контура

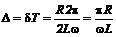. (10)

Если за N колебаний амплитуда уменьшается в е раз, то соответствующее этому уменьшению время называется временем релаксации t:

Отсюда следует

. (11)

За время релаксации система совершает N колебаний

. (12)

Логарифмический декремент затуханий можно определить, следовательно, как величину, обратную числу колебаний, совершаемых за время релаксации. Для характеристики колебательной системы часто применяют величину, обратно пропорциональную D.

. (13)

Добротность контура определяется с помощью соотношения:

. (14)

Чем меньше логарифмический декремент затухания, тем выше добротность контура.

Из формул (13) и (14) следует , то есть, чем больше колебаний успевает совершить система прежде чем амплитуда уменьшится в n раз, тем добротность колебательной системы выше. В случае малых потерь энергии добротность определяет во сколько раз энергия, запасённая в контуре, больше средней потери энергии за промежуток времени, в течение которого фаза колебаний меняется на 1 радиан.

. (15)

Добротность колебательного контура, с учётом малых потерь энергии:

. (16)

Не нашли, что искали? Воспользуйтесь поиском: