Электромагнитная теория Максвелла

Вследствие наличия электрического сопротивления в реальном колебательном контуре электромагнитные колебания носят затухающий характер.

Для того, чтобы колебания были незатухающими, необходимо непрерывно пополнять запас энергии. Это можно сделать, подключив к контуру источник переменного напряжения. В пространстве, окружающем контур, возникает переменное электромагнитное поле, которое распространяется в виде электромагнитной волнысо скоростью света. В вакууме эта скорость равна 3×10⁸ м/с.

Причины распространения электромагнитной волны рассмотрены в электромагнитной теории Максвелла. Основу этой теории составляет система уравнений Максвелла.

Электромагнитная волна характеризуется векторами напряженности электрического и магнитных полей и описывается системой уравнений Максвелла:

, (1)

, (2)

Эти два уравнения показывают неразрывную связь между электрическим и магнитным полями. Физический смысл уравнения (1), являющегося обобщением закона электромагнитной индукции Фарадея, заключается в том, что всякое переменное магнитное поле 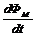создает вихревое электрическое поле. Вихревой характер электрического поля означает, что силовые линии поля замкнуты. Уравнение (2)говорит о том, что изменяющееся во времени электрическое поле между обкладками конденсатора создает вокруг себя вихревое магнитное поле. Заметим, что кроме приведенных выше двух уравнений Максвелла имеются еще пять, о которых мы говорить здесь не будем.

На рис. 2 показано возникновение электрического (рис. 2 а) и магнитного (рис. 2б)вихревых полей.

Одним из основных выводов теории Максвелла является то, что в колебательном контуре, по которому протекает переменный ток, наряду с током проводимости в проводнике, характеризуемом плотностью тока проводимости 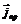в силу непрерывности тока должен существовать ток и в конденсаторе, равный току проводимости. Этот ток представляет собой переменное электрическое поле и характеризуется вектором плотности тока смещения (рис. 3).

Еще одним важным выводом теории Максвелла является то, что переменное электромагнитное поле не может оставаться неподвижным и будет распространяться в окружающее пространство. Переменные электрические и магнитные поля не могут существовать независимо одно от другого: одно поле порождает другое. Оба поля, электрическое и магнитное, имеют вихревой характер: силовые линии замкнуты и притом переплетены, электрические линии оборачиваются около магнитных, а магнитные – около электрических. Некоторое представление о характере электромагнитного поля может быть дано изображением его в виде цепочки колец – чередующихся замкнутых магнитных и электрических силовых линий (рис. 4).

Цепочка существует только в том случае, если поле – переменное. Нарастающий кольцевой магнитный поток создает вокруг себя электрический кольцевой поток, а изменение электрического поля приводит к созданию кольцевого магнитного потока и т.д. Так происходит распространение электромагнитной волны. Эта волна характеризуется векторами напряженности электрического поля и магнитного полей совершающими гармонические колебания с одинаковой частотой.

,

где и – амплитудные значения их напряженностей;

w – циклическая частота;

k – волновое число, (k = 2p/l);

l – длина волны.

На рис. 5. изображена плоская электромагнитная волна.

Викторы и совершают колебания во взаимно перпендикулярных плоскостях, всегда перпендикулярны вектору скорости распространения волны .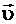

Для дальнейших рассуждений можно ограничиться рассмотрением только вектора напряженности электрического поля (рис. 6).

Расстояние, на которое распространяется волна за время одного периода Т колебаний вектора , называется длиной волны l, т. е.

l = υT,

где υ – скорость волны.

Частота колебаний n равна

n = ,

поэтому

.

Не нашли, что искали? Воспользуйтесь поиском: