Основные законы термодинамики

Термодинамика первоначально возникла как наука о превращениях теплоты в работу. Однако законы, лежащие в основе термодинамики, имеют настолько общий характер, что в настоящее время термодинамические методы с большим успехом применяются для исследования многочисленных физических и химический процессов и для изучения свойств вещества и излучения. Как уже отмечалось, при изучении свойств и процессов превращения вещества термодинамика не вдается в рассмотрение микроскопической картины явлений. Она рассматривает явления, опираясь на извлеченные из опыта основные законы (начала). По этой причине выводы, к которым приходит термодинамика, имеют такую же степень достоверности, как и лежащие в ее основе законы. Последние же являются обобщением огромного количества опытных данных.

Основу термодинамики образуют два ее начала. Первое начало устанавливает количественные соотношения, имеющие место при превращениях энергии из одних видов в другие. Второе начало определяет условия, при которых возможны эти превращения, т. е. определяет возможные направления процессов.

Первое начало термодинамики утверждает, что количество тепла, сообщаемое системе, затрачивается на приращение внутренней энергии системы и совершение системой работы над другими телами:

(1.92)

или в дифференциальной форме

. (1.93)

Первое начало иногда формулируется следующим образом: невозможен перпетуум мобиле (вечный двигатель) первого рода, т. е. такой периодически работающий двигатель, который совершал бы работу в большем количестве, чем получаемая извне энергия.

Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс (цикл). Пусть в ходе цикла рабочее тело (например, газ) сначала расширяется до объема V ₂, а затем снова сжимается до первоначального объема V ₁ (рис. 1.21). Чтобы работа за цикл была больше нуля, давление (а следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему телу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту.

Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество тепла, сообщаемое рабочему телу за цикл, равно , где – теплота, получаемая рабочим телом при расширении, а – теплота, отдаваемая при сжатии. Работа A, совершаемая за цикл, равна площади цикла. Таким образом, выражение (1.92), написанное для цикла, имеет вид:

. (1.94)

Периодически действующий двигатель, совершающий работу за счет получаемой извне теплоты, называется тепловой машиной. Как следует из (1.94), не вся получаемая извне теплота Q ₁ используется для получения полезной работы. Для того чтобы двигатель работал циклами, часть теплоты, равная , должна быть возвращена во внешнюю среду, т.е. не используется по назначению (для совершения полезной работы). Очевидно, что чем полнее превращает тепловая машина получаемую извне теплоту Q ₁ в полезную работу A, тем эта машина выгоднее. Поэтому тепловую машину принято характеризовать коэффициентом полезного действия η (сокращенно КПД), который определяется как отношение совершаемой за цикл работы A к получаемой за цикл теплоте Q ₁

. (1.95)

Приняв во внимание соотношение (20.3), выражение для к.п.д. можно записать в виде

. (1.96)

Из определения КПД следует, что он не может быть больше единицы.

Если обратить цикл, изображенный на рис. 1.21, получится цикл холодильной машины. Такая машина отбирает за цикл от тела с температурой T ₂ количество тепла Q ₂ и отдает телу с более высокой температурой T ₁ количество тепла . Над машиной за цикл должна быть совершена работа A ′. Эффективность холодильной машины характеризуют ее холодильным коэффициентом, который определяют как отношение отнятого от охлаждаемого тела количества теплоты Q ₂ к работе A ′, которая затрачивается на приведение машины в действие:

холодильный коэффициент .

Второе начало термодинамики, как и первое, может быть сформулировано несколькими способами. С одной из формулировок мы познакомились в п.1.21. Оно заключается в утверждении о том, что энтропия изолированной системы не может убывать.

. (1.97)

Клаузиус сформулировал второе начало следующим образом: невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела менее нагретого к телу более нагретому. Не следует представлять дело так, что второе начало вообще запрещает переход тепла от тела менее нагретого к телу более нагретому. В холодильной машине как раз совершается такой переход. Однако этот переход не является единственным результатом процесса. Он сопровождается изменениями в окружающих телах, связанными с совершением над системой работы A ′.

Покажем, что совершаемый в изолированной системе воображаемый процесс, противоречащий второму началу в формулировке Клаузиуса, сопровождается уменьшением энтропии. Тем самым мы докажет эквивалентность формулировки Клаузиуса и статистической формулировки второго начала, согласно которой энтропия изолированной системы не может убывать.

Предварительно сделаем следующее замечание. Допустим, что некоторое тело обменивается теплом с другим телом, которое мы будем называть тепловым резервуаром. Пусть теплоемкость резервуара бесконечно велика. Это означает, что получение или отдача резервуаром конечного количества тепла не изменяет его температуры. Протекающий в теле процесс, сопровождающийся обменом теплом с резервуаром, может быть обратим только в том случае, если в ходе этого процесса температура тела будет равна температуре соответствующего резервуара. В самом деле, если, например, тело получает тепло от резервуара с температурой T ₁, имея температуру, меньшую чем T ₁, то при протекании того же процесса в обратном направлении тело сможет вернуть резервуару полученное от него тепло в том случае, если его температура во всяком случае не ниже чем T ₁. Следовательно, при прямом и обратном ходе процесса температура тела будет различна, тело проходит в обоих случаях через различные последовательности состояний (характеризующиеся неодинаковыми температурами), и рассматриваемый процесс будет необратимым.

Таким образом, процесс, сопровождающийся теплообменом, может быть необратимым только в том случае, если, получая тепло и возвращая его при обратном ходе резервуару, тело имеет одну и ту же температуру, равную температуре резервуара. Строго говоря, при получении тепла температура тела должна быть на бесконечно малую величину меньше температуры резервуара (иначе тепло не потечет от резервуара к телу), а при отдаче тепла температура тела должна быть на бесконечно малую величину выше температуры резервуара.

Следовательно, единственным обратимым процессом, сопровождающимся теплообменом с резервуаром, температура которого остается неизменной, является изотермический процесс, протекающий при температуре резервуара.

Рассмотрим изолированную систему, состоящую из двух тел с одинаковой теплоемкостью C. Пусть тело B передает телу A количество тепла Q, в результате чего температура тела A повышается от значения T_A0 до T_A, а температура тела B уменьшается от значения T_B0 до T_B (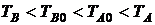). Такой процесс противоречит второму началу в формулировке Клаузиуса. Найдем изменение энтропии в данном случае.

В ходе указанного процесса происходит теплообмен между телами с неодинаковыми температурами. Согласно сказанному выше такой процесс необратим. Для того чтобы найти изменение энтропии при необратимом процессе, поступают следующим образом. Рассматривают какой-либо обратимый процесс, приводящий систему в то же конечное состояние, что и данный необратимый процесс, и вычисляют для этого процесса приращение энтропии по формуле

. (1.98)

В соответствии со сказанным выше рассмотрим обратимый процесс, в ходе которого тело B отдает теплоту Q порциями 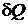последовательно ряду резервуаров с температурами, имеющими все значения от T_B0 до T_B, а тело A получает тепло Q порциями от ряда резервуаров с температурами от T _A0 до T_A. В результате система перейдет обратимо из состояния, в котором тела имеют температуры T_A0 и T_{B 0}, в состояние, в котором температуры тел равны T _A и T_B. Приращение энтропии в ходе этого процесса равно

.

Приняв во внимание, что , (), представим Δ S в виде

.

Поскольку , выражение в скобках меньше единицы и, следовательно, . Таким образом, мы показали, что в ходе воображаемого процесса, противоречащего второму началу в формулировке Клаузиуса, энтропия убывает, что противоречит закону неубывания энтропии.

Кельвину принадлежит еще одна формулировка второго начала термодинамики. Она звучит следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла полностью в работу.

На первый взгляд может показаться, что такой формулировке противоречит, например, процесс изотермического расширения идеального газа. Действительно, все полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение тепла и превращение его в работу – не единственный конечный результат процесса; кроме того, в результате процесса происходит изменение объема газа.

В тепловой машине превращение тепла в работу обязательно сопровождается дополнительным процессом – передачей некоторого количества тепла более холодному телу, вследствие чего получаемое от более нагретого тела количество тепла не может быть превращено полностью в работу.

Легко убедиться в том, что утверждение, содержащееся в формулировке Кельвина, логически вытекает из утверждения, заключающегося в формулировке Клаузиуса. В самом деле, работа может быть полностью превращена в тепло, например, при посредстве трения. Поэтому, превратив с помощью процесса, запрещенного формулировкой Кельвина, тепло, отнятое от какого-нибудь тела, полностью в работу, а затем, превратив эту работу при посредстве трения в тепло, сообщаемое другому телу с более высокой температурой, мы осуществили бы процесс, невозможный согласно формулировке Клаузиуса.

Используя процессы, запрещаемые вторым началом термодинамики, можно было бы создать двигатель, совершающий работу за счет тепла, получаемого от такого, например, практически неисчерпаемого источника энергии, как океан. Практически такой двигатель был бы равнозначен вечному двигателю. Поэтому второе начало термодинамики иногда формулируется следующим образом: невозможен перпетуум мобиле второго рода, т. е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.

Цикл Карно

Из сказанного в предыдущем параграфе следует, что для работы теплового двигателя необходимо наличие двух тепловых резервуаров. От одного из них, имеющего более высокую температуру T ₁ и называемого нагревателем, двигатель получает в ходе цикла количество теплоты Q ₁; второму, имеющему более низкую температуру T ₂ и называемому холодильником, двигатель отдает количество теплоты .

Допустим, что теплоемкость резервуаров бесконечно велика. Это означает, что получение или отдача резервуарами конечного количества теплоты не изменяет их температуры. Выясним, какой обратимый цикл может совершать рабочее вещество двигателя в этих условиях. Для краткости рабочее вещество двигателя мы будем называть просто телом.

Рассматриваемый цикл, очевидно, может состоять как из процессов, в ходе которых тело обменивается теплом с резервуарами, так и из процессов, не сопровождающихся теплообменом с внешней средой, т. е. адиабатических процессов. В предыдущем параграфе мы установили, что единственным обратимым процессом, сопровождающимся теплообменом с резервуаром, температура которого остается неизменной, является изотермический процесс, протекающий при температуре резервуара.

Таким образом, мы приходим к выводу, что обратимый цикл, совершаемый телом, вступающим в теплообмен с двумя тепловыми резервуарами бесконечно большой емкости, может состоять только из двух изотерм (при температурах резервуаров) и двух адиабат. Такой цикл был впервые введен в рассмотрение французским инженером Сади Карно и носит название цикла Карно. Отметим, что цикл Карно по определению обратимый.

При адиабатическом процессе 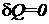, поэтому и, следовательно, энтропия остается постоянной. На этом основании обратимый адиабатический процесс называется изоэнтропическим. Воспользовавшись этим термином, можно сказать, что цикл Карно состоит из двух изотерм и двух изоэнтроп. На диаграмме T, S этот цикл выглядит так, как показано на рис. 1.23. Заметим, что вид цикла Карно на диаграмме T, S не зависит от свойств тела (или системы тел), для которых он изображен.

На рис. 1.23 изображен некоторый процесс, переводящий систему из состояния 1 в состояние 2. Элементарное количество тепла 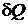, полученное системой, может быть представлено в виде . Следовательно, площадь заштрихованной полоски на рис. 1.23 равна 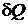, а площадь фигуры, ограниченной кривой 1 – 2, дает количество теплоты, получаемое системой в ходе процесса. Аналогично площадь фигуры, ограниченной кривой, изображающей процесс на диаграмме p, V, дает работу, совершаемую системой в ходе процесса (см. рис.1.4).

В соответствии со сказанным площадь цикла (рис. 1.23) дает количество теплоты, получаемой системой в ходе цикла (оно равно 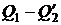). Аналогично площадь цикла на диаграмме p, V дает работу, совершаемую системой за цикл (см. рис. 1.5).

Количество теплоты, получаемой системой в ходе произвольного обратимого процесса, можно вычислить по формуле

. (1.99)

Найдем КПД цикла Карно. Совершив цикл, система возвращается в исходное состояние. Следовательно, полное изменение энтропии за цикл равно нулю. На участке 1 – 2 (см. рис. 1.22) система получает от резервуара с температурой T ₁ количество теплоты Q ₁. Приращение энтропии на этом участке равно

.

На участке 3 – 4 система отдает резервуару с температурой T ₂ количество тепла . Отнятие у тела теплоты эквивалентно сообщению тепла 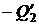. Поэтому приращение энтропии на участке 3 – 4 равно

.

На участках 1 – 2 и 4 – 1 энтропия постоянна. Таким образом, полное приращение энтропии за цикл равно

. (1.100)

Из (1.100) следует, что

. (1.101)

Выражение (1.95) для КПД тепловой машины можно представить в виде

. (1.102)

Заменив в этом выражении отношение в соответствии с (1.101), получим, что

. (1.103)

При выводе формулы (1.103) мы не делали никаких предположений о свойствах рабочего тела и устройстве тепловой машины. Следовательно, мы приходим к утверждению, что коэффициент полезного действия всех обратимых машин, работающих в идентичных условиях (т. е. при одной и той же температуре нагревателя и холодильника), одинаков и определяется только температурами нагревателя и холодильника. Это утверждение носит название теоремы Карно.

Рассмотрим необратимую машину, работающую с теми же нагревателем и холодильником, что и обратимая машина, работающая по циклу Карно. Пусть по завершении цикла машина возвращается в исходное состояние, которое мы будем считать равновесным. Так как энтропия является функцией состояния, ее приращение за цикл должно равняться нулю

.

Поскольку процессы, из которых состоит цикл, необратимы, для каждого элементарного процесса имеет место неравенство . Следовательно, из условия равенства нулю полного приращения энтропии за цикл вытекает, что

,

откуда

.

Разобьем последний интеграл на четыре слагаемых:

.

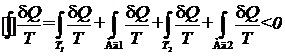Первое слагаемое отвечает процессу получения от резервуара с температурой Т₁ количество теплоты Q₁ (это количество теплоты не обязательно совпадает с количеством теплоты Q₁, которое получает за цикл обратимая машина). Второе слагаемое отвечает первому адиабатическому участку цикла. Третье слагаемое отвечает процессу передачи теплоты резервуару с температурой Т₂ (это количество теплоты не обязательно совпадает с количеством теплоты , которое отдает за цикл обратимая машина). Наконец, четвертое слагаемое отвечает второму адиабатическому участку цикла. На адиабатических участках , поэтому соответствующие интегралы равны нулю. Интеграл, отвечающий участку Т₁, равен (напомним, что в случае необратимого процесса в знаменателе отношения стоит температура резервуара, от которого данное тело получает теплоту 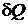). Интеграл, отвечающий участку Т₂, равен . Таким образом, мы приходим к неравенству

. (1.104)

Из (1.104) получаем, что

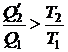
и, следовательно,

. (1.105)

Полученный результат означает, что КПД необратимой машины всегда меньше, чем обратимой, работающей в тех же условиях.

Вид цикла Карно на диаграмме p,V зависит от свойств рабочего тела, совершающего цикл. Для идеального газа цикл выглядит так, как показано на рис. 1.24. Коэффициент полезного действия цикла Карно для идеального газа можно вычислить, не прибегая к нахождению приращения энтропии.

При изотермическом процессе внутренняя энергия идеального газа остается постоянной. Поэтому количество полученной газом теплоты Q₁ равно работе A₁₂, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 1.24). Эта работа согласно (1.60) равна

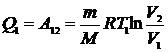, (1.106)

где m – масса идеального газа в машине. Количество отдаваемой холодильнику теплоты равно работе , затрачиваемой на сжатие газа при переводе его из состояния 3 в состояние 4. Эта работа равна

. (1.107)

Для того чтобы цикл был замкнутым, состояния 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие

. (1.108)

(см. уравнение адиабаты (1.41)). Аналогично, поскольку состояния 2 и 3 лежат на одной и той же адиабате, выполняется условие

. (1.109)

Деля (1.109) на (1.108), приходим к условию замкнутости цикла

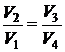. (1.110)

Теперь подставим (1.106) и (1.107) в выражение (1.96) для КПД:

.

Наконец, учтя условие (1.110), получим выражение (1.96) для КПД:

,

которое совпадает с (1.103).

Не нашли, что искали? Воспользуйтесь поиском: