Уравнение состояния газа. Процессы.

Факультет вычислительной математики и кибернетики

Кафедра прикладной математики

ЗАДАЧИ ПО ТЕРМОДИНАМИКЕ

И МОЛЕКУЛЯРНОЙ ФИЗИКЕ

Нижний Новгород - 2005 г.

УДК 537. ЗАДАЧИ ПО ТЕРМОДИНАМИКЕ И МОЛЕКУЛЯРНОЙ ФИЗИКЕ

Сост. В.Н. Комаров, А.Г. Панасенко

Нижний Новгород: ННГУ. 2004. 24 с.

«ЗАДАЧИ ПО ТЕРМОДИНАМИКЕ И МОЛЕКУЛЯРНОЙ ФИЗИКЕ» пред­назначены для студентов 2-3 курсов факультета ВМК.

Пособие предназначено в первую очередь для студентов вечерней формы обучения на факультете ВМК ННГУ. Задачи подобраны в соответствии с учебной программой по физике и в течение нескольких лет использовались авторами для аудиторных занятий и самостоятельной работы студентов вечернего отделения ф-та ВМК ННГУ. В пособии собраны как базовые задачи, так и контрольные вопросы для закрепления материала и самопроверки. Задачи служат закреплению материала лекций и способствуют более глубокому пониманию законов физики.

Составители:

Доктор технических наук,

профессор В.Н. Комаров,

кандидат физ.-мат. наук,

доцент А.Г. Панасенко

Рецензент:

Доктор физ.-мат. наук,

профессор В.В. Новиков

Нижегородский государственный университет

им. Н.И. Лобачевского, 2004

ПРЕДИСЛОВИЕ

В настоящем пособии собраны задачи, многие из которых использовались авторами на практических занятиях по курсу общей физики "Термодинамика и молекулярная физика", предлагались для самостоятельной работы студентов. Эти задачи, охватывая бόльшую часть разделов курса, должны способствовать более глубокому усвоению материала.

На первых порах студенты могут пользоваться приведенными в начале каждого раздела основными формулами, используемыми при решении задач. Постепенно же эти формулы нужно запоминать, так как тогда основное внимание можно уже сосредоточить на физическом содержании задачи, не тратя время на поиск подходящих формул.

Приведенные в пособии задач допускают аналитическое решение, т. е. позволяют получить расчетные формулы, в которых неизвестные искомые величины выражены через данные задачи. Обязательно проверяйте размерность полученных формул, пробуйте применить их к простейшим предельным случаям, которые вы знаете, и только после этого проводите численные расчеты. Сравнение полученных результатов с приведенными ответами к задачам, позволит обнаружить ошибку, если она есть, или убедиться в правильности рассуждений и расчетов.

Успехов Вам!

P.S. Любые Ваши замечания и пожелания, касающиеся пособия, будут авторами внимательно рассмотрены, если вы сообщите их на кафедру прикладной математики факультета ВМК ННГУ.

Составители

Уравнение состояния газа. Процессы.

· Уравнение состояния идеального газа:

,

где р - давление: V – объем; Т - абсолютная температура; m – масса; μ - молярная масса; R = 8,314 Дж/кмоль – универсальная газовая постоянная.

· Уравнение состояния ван-дер-ваальсовского газа (для одного моля):

,

где V - объем, занимаемый молем газа при данных р и Т, а и b - посто­янные Ван-дер-Ваальса для данного газа.

· Закон Дальтона: давление смеси идеальных газов равно сумме пар­циальных давлений (парциальное давление - это давление, которое ока­зывал бы на стенки сосуда один газ смеси в отсутствие остальных).

· Зависимость давления газа от высоты в поле силы тяжести в изо­термическом приближении дается барометрической формулой:

,

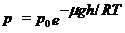где р ₀ - давление на высоте h = 0, g = 9,8 м/с² - ускорение свободного падения.

1.1. Найти плотность ρ двухатомного кислорода при давлении p = 50 aтм и температуре t = 27° С.

Ответ: ρ = μр / RТ = 0,065 г/см³.

1.2. Каков может быть минимальный объем баллона, вмещающего 6,4кг кислорода, если его стенки при температуре 20^о C выдерживают давление в 17 н/см².

Ответ: м³.

1.3. Давление воздуха внутри плотно закупоренной бутылки при температуре 7^о C было равно 1 атм. При нагревании бутылки пробка вылетела. Найти, до какой температуры нагрели бутылку, если известно, что пробка вылетела при давлении воздуха в бутылке, равном 1,3 атм.

Ответ: 390 К.

1.4. Из баллона вследствие неисправности вытекает водород. Объем баллона 20 л. Первона­чальное давление 10,2 атм в результате убыли газа уменьшается до 4,957 атм. Вместе с этим газ охлаждается с 127^o C до 27^o C. Определить, какое количество водорода вытекло. Газ считать идеальным.

Ответ: 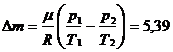г.

1.5. Из баллона вследствие неисправности вытекает водород. Объем баллона 20 л. Первона­чальное давление 10,2 атм в результате убыли газа уменьшается до 4,957 атм. Вместе с этим газ охлаждается с 127^o C до 27^o C. Определить, сколько молекул газа ушло из бал­лона. Газ считать идеальным.

Ответ: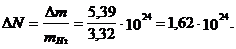

1.6. Плотность ρ воздуха при температуре 0° С и давлении 760 мм рт. ст. равна 0,001293 г/см³. Определить массу литра воздуха при температуре 27,3° С и давлении 750 мм рт. ст.

Ответ: m = 1,15 г.

1.7. Электрическая газонаполненная лампа накаливания наполнена азотом при давлении в 600 мм рт. ст.Емкость лампы 500 см³. Какое количество воды войдет в лампу, если у нее отломить кончик под водой при нормальном атмосферном давлении?

Ответ: m = 105 г.

1.8. Найти молекулярный вес смеси, состоящей из 20 весовых процентов кислорода, 70 весо­вых процентов азота и 10 процентов углекислого газа. Определить плотность этой смеси при нормальных условиях.

Ответ: 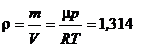кг/м³

где

1.9. Смесь газов состоит из 30 г азота и некоторого количества углекислого газа, так что мо­лекулярный вес смеси равен 32. Определить количество углекислого газа в смеси.

Ответ: г.

1.10. Давление воздуха в велосипедной камере при температуре 7^о С равно 150 смртутного столба. Определить, каково будет давление, если температура повысится до 32^о С. Счи­тать объем камеры неизменным.

Ответ: см. рт. ст.

1.11. Подсчитать, как сильно отличается масса автомобильной шины летом, при t ^о = 30^о С, и зимой, при t ^о = -30^о С. Давление в шине зимой и летом 3 атм. Объем шины считать не­изменным и равным 50 л. Масса одного литра воздуха при нормальных условиях равна 1,29 г/л.

Ответ: г.

1.12. Конец открытой стеклянной метровой (l = 1 м) трубки, бóльшая часть которой погружена в ртуть, выступает на h = 12 см над поверхностью ртути. Трубку закрывают и вынимают из ртути. Какую часть трубки будет занимать ртуть после поднятия? Атмосферное давление 750 мм рт ст.

Ответ: 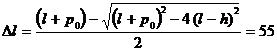см.

1.13. Узкая цилиндрическая трубка, закрытая с одного конца, содер­жит воздух, отделенный от наружного воздуха столбиком ртути длиной h (мм). Когда трубка обращена закрытым концом кверху, воздух вну­три нее занимает длину l, когда же трубка обращена кверху открытым концом, то воздух внутри нее занимает длину l ' < l. Определить атмо­сферное давление Н (мм рт. ст.).

Ответ: Н = h (l + l ')/(l - l ').

1.14. Два одинаковых баллона соединены трубкой с клапаном, про­пускающим газ из одного баллона в другой при разности давлений Δ_p ≥ l,l aтм. Сначала в одном баллоне был вакуум, а в другом иде­альный газ при температуре t ₁ = 27° С и давлении р ₁ = 1 атм. Затем оба баллона нагрели до температуры t ₂ = 107° С. Найти давление газа в баллоне, где был вакуум.

Ответ: 0,1 атм.

1.15. Сосуд объемом V = 20 л содержит смеcь водорода и гелия при температур t = 20° С и давлении р = 2 атм. Масса смеси m = 5 г. Найти отношение массы водорода к массе гелия в данной смеси.

Ответ: (гр)

1.16. В сосуде находится смесь m ₁ = 7 г азота и m ₂ = 11 г углеки­слого газа при температуре Т = 290 K и давлении р ₀ = 1 атм. Найти плотность этой смеси, считая газы идеальными.

Ответ: 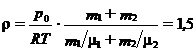г/л

1.17. При одном качании компрессор захватывает V ₀ = 2 л воздуха при атмосферном давлении и температуре t ₁ = 3^о С.Сколько качаний должен сделать компрессор, чтобы увеличить вдвое давление в сосуде емкостью V = 1000 л, если температура воздуха в нем поддерживается рав­ной t ₂ = 27^о С и начальное давление вне и внутри сосуда одинаково?

Ответ:

1.18. В вертикальном, закрытом с обоих торцов цилиндра, находится массивный поршень, по обе стороны которого по одному молю воздуха. При Т ₁ = 300 K отношение верхнего объема к нижнему ŋ₁ = 4. При какой температуре это отношение станет ŋ₂ = 3? Трение не учитывать.

Ответ: .

1.19. В гладкой открытой с обоих концов вертикальной трубе, име­ющей два разных сечения (см. рис.). находятся два поршня, соединен­ные нерастяжимой нитью, а между поршнями - один моль идеального газа. Площадь сечения верхнего поршня на Δ S = 10 см2 боль-	Рис. 1.
больше, чем нижнего. Общая масса поршней т = 5 кг. Давление наружного воздуха p 0 = 1 атм. На сколько кельвин надо нагреть газ между поршнями, чтобы они переместились на l = 5 см? Ответ: Δ T = (mg + p 0·Δ S) l / R = 0,9 K.

1.20. Поршневым воздушным насосом откачивают сосуд объемом V. За один цикл (ход поршня) насос захватывает объем Δ V. Через сколько циклов давление в сосуде уменьшится в η раз? Процесс считать изотер­мическим, газ - идеальным.

Ответ: п = ^ln(η)/_{ln(l + Δ V / V )}.

1.21. Найти давление воздуха в откачиваемом сосуде как функцию времени откачки t. Объем сосуда V, первоначальное давление p ₀. Процесс считать изотермическим и скорость откачки не зависящей от давления и равной С.(Скоростью откачки называют объем газа, откачиваемый за единицу времени, причем этот объем измеряется при давлении газа в данный момент).

Ответ: p = p ₀exp(- ct/V).

1.22. Найти максимально возможную температуру идеального газа в каждом из нижеследующих процессов:

а) р = α р ₀ V ²;

б) p = p ₀ e^{- β V},

где р ₀, α, β - положительные постоянные; V - объем моля газа.

Ответ: a) ; б) T _max = p ₀/ eRβ.

1.23. Допустим, давление р и плотность ρ воздуха связаны соотноше­нием ρ = const∙ р^п независимо от высоты (здесь п - постоянная). Найти соответствующий градиент температуры.

Ответ: .

1.24. Считая, что температура и молярная масса воздуха, а также ускорение свободного падения не зависят от высоты, найти разность вы­сот, на которых плотности воздуха при температуре 0° С отличаются: а) в е раз; б) на η = 1%.

Ответ: a) h = RT / μg = 8 км; б) h = μRT / ηg = 0,8 км.

1.25. Какому давлению необходимо подвергнуть углекислый газ при температуре Т = 300 K, чтобы его плотность оказалась равной ρ = 500 г/л? Расчет провести как для идеального газа, так и для ван-дер-ваальсовского.

Ответ: р _ид 280 атм; р _ВдВ 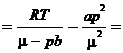80 атм.

1.26. Один моль азота находится в объеме V = 1 л.Найти температуру азота, при которой погрешность в давлении, определяемом уравнением состояния идеального газа, составляет η = 10%по сравнению с давлени­ем ван-дер-ваальсовского газа.

Ответ: Т = a(V - b)( 1 + η)/ RV (ηV + b) = 133 K.

1.27. Изобразить для идеального газа примерные графики изохорического, изобарического и изотермического процессов на диаграммах: а) p, V; б) Т, V; в) Т, р. Графики изобразить проходящими через общую для них точку.

1.28. На рисунке изображены две изотермы для одной и той же массы идеального газа. Какая из температур больше?
1.29. На рисунке изображен круговой процесс в координатах (р, V). Кри­волинейные участки – изотермы. Изобразить тот же процесс в коорди­натах (р, Т) и (V, Т).

1.30. Пользуясь уравнением pV = RT, убедиться в справедливости соотношения

Не нашли, что искали? Воспользуйтесь поиском: