Первое начало термодинамики.

Теплоемкость.

· Первое начало термодинамики:

Q = Δ U + A,

где Q - количество тепла, сообщенное системе; А - работа, совершаемая системой; Δ U - приращение внутренней энергии системы.

· Работа, совершаемая газом:

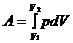
· Теплоемкость системы:

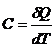
· Уравнение Майера:

C_p – C_V = R

где C _p, C _V - молярные теплоемкости при постоянных давлении и объеме соответственно.

· Внутренняя энергия идеального газа:

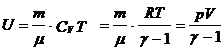
· Молярная теплоемкость идеального газа при политропическом про­цессе:

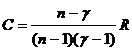
· Внутренняя энергия моля газа Ван - дер - Ваальса:

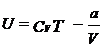
2.1. Газообразный водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л. охладили на Δ T = 55 K. Найти приращение внутренней энергии газа и количество отданного им тепла.

Ответ: 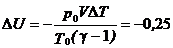кДж;

2.2. Какое количество тепла надо сообщить азоту при изобарическом нагревании, чтобы газ совершил работу A, равную 2 Дж?

Ответ: Дж.

2.3. Газ, занимающий объем 5 л и находящийся под давлением 2·10² Н/м² при температуре 17^о C, был нагрет и расширялся изобарически. Работа расширения газа при этом оказалась равной 196 Нм. На сколько нагрели газ?

Ответ: K

2.4. На нагревание 40 г кислорода от 16^о Cдо40^о Cзатрачено 150 кал. При каких условиях нагре­вался газ? (При постоянном объеме или при постоянном давлении?)

Ответ: при постоянном объеме, т. к.

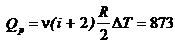Дж; Дж.

2.5. Найти молярную массу газа μ, если при нагревании m = 0,5 кг этого газа на Δ T = 10 K изобарически требуется на Δ Q = 1,48 кДжтепла больше, чем при изохорическом нагревании.

Ответ: μ = mR Δ T /Δ Q = 28 г/моль.

2.6. Один моль некоторого идеального газа изобарически нагрели на Δ T = 72 K, сообщив ему количество тепла Q = 1,6 кДж.Найти прира­щение его внутренней энергии и величину γ = С_p / C_V.

Ответ: Δ U = Q - R Δ T = 1 кДж; γ = Q/ (Q - R Δ T) = 1,6.

2.7. Вычислить γдля газовой смеси, состоящей из v ₁= 2 моля кисло­рода и v ₂ = 3 моля углекислого газа. Газы считать идеальными.

Ответ: γ = [ v ₁ γ ₁(γ ₂ - 1) + v ₂ γ ₂(γ ₁ - 1)]/[ v ₁ (γ ₂ - 1 ) + v ₂(γ ₁ - 1)] = 1,33.

2.8. Вычислить удельные теплоемкости C_p и С_V для газовой смеси, состоящей из 7 г азота и 20 г аргона. Газы идеальные.

Ответ: С_р = 0,65 Дж/(г∙К); C_V = 0,42 Дж/(г∙К).

2.9. Найти удельные теплоемкости c_v и c_p некоторого газа, если известно, что масса одного киломоля этого газа равна μ = 30 кг/кмоль и отношение γ = c_p/c_v = 1,4.

Ответ:

Дж/кг; 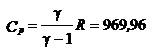Дж/кг.

2.10. При изобарическом расширении кислорода им была совершена работа A = 2·10^-6 Дж. Оп­ределить изменение внутренней энергии Δ U этого количества газа, количество тепла Q, сообщенного ему в процессе расширения, а также массу газа m, если его температура возросла на 10^о. Газ считать идеальным.

Ответ: ;

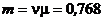мкг;

Δ U = ν C _VΔ T = (⁵/₂)ν R Δ T = 4,99∙10^-6 Дж;

Q = ν C _pΔ T = (⁷/₂)ν R Δ T = 6,99∙10^-6 Дж.

2.11. Газ находится в вертикально расположенном цилиндре с площадью дна s = 10 см². Пор­шень, закрывающий цилиндр, имеет массу 10 кги может перемещаться в цилиндре без трения. Начальный объем газа 8 л, температура 10^о С. Какое количество тепла необхо­димо затратить для того, чтобы нагреть газ при этих условиях на 25^о С, если известно, что теплоемкость C_V этой массы газа, измеренная при закрепленном в начальном положении поршне, оказалась равной 25 дж/град? Давление наружного воздуха не учитывать.

Ответ: 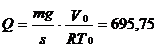Дж.

2.12. В сосуде под поршнем находится m ₀ = 10 г азота. 1) Какое количество тепла Q надо затратить, чтобы нагреть азот на Δ t ^o = 20^о С? 2) На сколько при этом поднимается поршень? Масса поршня m = 1 кг, площадь поперечного сечения s = 10 см². Давление над поршнем равно 1 атм.

Ответ: Q = ν C Δ t ^o = 20785 Дж; 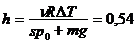м.

2.13. 2 л азота находятся под давлением 10⁵ н/м². Какое количество тепла надо сообщить азоту, чтобы при p = const объем увеличить вдвое?

Ответ: Q =pC_pV/R = 700 Дж.

2.14. 2 л азота находятся под давлением 10⁵ н/м². Какое количество тепла надо сообщить азоту, чтобы при V = const давление увеличить вдвое?

Ответ: Q = C_VVp/R = 500 Дж.

2.15. Найти молярную теплоемкость идеального газа при политропическом процессе pV ⁿ = соnst, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

Ответ: С = Р (п -γ) / (n - 1)(γ - 1); С < 0 при 1 < n < γ.

2.16. Имеется идеальный газ, молярная теплоемкость С_V которого из­вестна. Найти молярную теплоемкость этого газа как функцию его объ­ема V, если газ совершает процесс по закону:

а) Т = T ₀ e ^αV; б) р = p ₀e^αV, где T ₀, p ₀, α-постоянные.

Ответ: а) С = C_V + R/ α V; б) С = С_V + R /(1 + α V).

2.17. Один моль идеального газа, теплоемкость которого при постоян­ном давлении С_p, совершает процесс по закону p = р ₀ + α/ V, где р ₀, α - постоянные. Найти:

а) теплоемкость газа как функцию его объема V;

б) сообщенное газу тепло при его расширении от V ₁до V ₂.

Ответ: a) C = γ R /(γ - 1) + α R / p ₀ V;

б) Q = p ₀(V ₂ – V ₁) C _P/ R + αln(V ₂/ V ₁).

2.18. Найти уравнение процесса (в переменных Т, V). при котором молярная теплоемкость идеального газа изменяется по закону:

а) С = С_V + αТ;

б) С = С_V + βТ;

в) С = С_V + ap.

Здесь α, β, а - постоянные.

Ответ: a) Ve^{- α T/R} = const; б) Ve^R/βV = const; в) V - аТ = const.

2.19. Один моль кислорода, находившегося при температуре T ₀ = 290 K, адиабатически сжали так, что его давление возросло в η = 10 раз. Найти:

а) температуру газа после сжатия;

б) работу, которая была совершена над газом.

Ответ: а) Т = T ₀ η ^(γ-1)/γ = 560 K;

б) A' = RT ₀(η ^1-1/γ - 1) / (γ - 1) = 5.6 кДж.

2.20. Некоторую массу азота сжали в η = 5 раз (по объему) один раз адиабатически, другой раз изотермически. Начальное состояние газа в обоих случаях одинаково. Найти отношение соответствующих работ, затраченных на сжатие.

Ответ: При адиабатическом сжатии работа больше в

n = (η^γ-1 – 1)/(γ – 1)lnη = 1,4 раза.

2.21. Объем моля идеального газа с показателем адиабаты γ изменяют по закону V = а/Т. где а - постоянная. Найти количество тепла, получен­ное газом в этом процессе, если его температура испытала приращение Δ T.

Ответ: Δ Q = R Δ T (2 - γ)/(γ - 1).

2.22. Найти работу, совершаемую одним молем ван-дер-ваальсовского газа при изотермическом расширении его объема от V ₁ до V ₂ при температуре Т.

Ответ: А = RТ ∙ln[(V ₂ - b)/(V ₁ – b)] + a/V ₂ - a/V ₁.

2.23. Один моль кислорода расширили от объема V ₁ = 1 л: до V ₂ = 5 л при постоянной температуре Т = 280 K. Вычислить количество погло­щенного газом тепла. (Газ считать ван-дер-ваальсовским.)

Ответ: Q = RТ ∙ln[(V ₂ - b)/(V ₁ – b)] = 3.8 кДж.

2.24. Найти для ван-дер-ваальсовского газа уравнение адиабаты в переменных (T, V), если его теплоемкость при постоянном объеме равна C_V.

Ответ: T (V - b) ^{R / Cv} = const.

2.25. Определить для ван-дер-ваальсовского газа разность моляр­ных теплоемкостей C_p – С_V.

Ответ: C _p – С_V = R /[l - 2 a (V - b)²/ RTV ³].

2.26. Показать, что между адиабатической и изотермической сжимаемостями (χ_{a д} = -(1/ V)∙(дV / дp), χ_T = -(1/ V)∙(дV / дp)_T) существует соотношение: χ _aд = χ _T /γ, где γ = C_p / C_V.

2.27. Показать, что если уравнение состояния имеет вид p = p (T, V), то справедливо соотношение: р α _р = K α _V, где

α _р = (др / дТ) _V / р - тепло­вой коэффициент давления при постоянном объеме,

α _V = (дV / дT) _p / V - коэффициент теплового расширения при постоянном давлении,

K = -V (др/дV)_Т - изотермический модуль упругости.

2.28. В цилиндре, закрытом с обоих концов и наполненном воздухом, находится поршень, разделяющий пространство в цилиндре на две рав­ные части. Давление воздуха по обе стороны поршня равно p ₀= 105 Пa. Поршень начинает совершать малые колебания, причем процесс в га­зе считаем адиабатическим. Масса поршня m = 1,5 кг, расстояние от стенки до поршня l = 20 см. площадь поршня S = 100 см². Трением пре­небрегаем. Определить период колебаний поршня.

Ответ: 0,05 с.

2.29 Моль идеального газа находится в неограниченном вертикальном цилиндре, помещенном в однородное поле тяжести. Найти теплоемкость газа.

Ответ: С = С_V + R = С_р.

2.30. Рассматривая воздух как идеальный газ, показать, что при на­гревании воздуха, находящегося в комнате, его внутренняя энергия не меняется, если только внешнее давление остается постоянным.

Ответ: результат следует из формулы U = С_VPV/R.

2.31. С какой высоты упал медный шар, если при столкновении с почвой его температура по­высилась с 20^оС до 23^оС?Считать, что выделившееся в результате столкновения коли­чество теплоты распределилось между медным шаром и почвой в соотношении 1: 2. Со­противлением воздуха пренебречь. С_м = 390 Дж/(кг∙К).

Ответ: h = 3 С_м Δ T / g = 358 м.

2.32. Внутренняя энергия теплового излучения в замкнутой полости с объемом V определяется выражением U = Vu,где плотность энергии и = аТ ⁴(постоянная а > 0), а давление излучения определяется уравнением состояния p = u /3. Найти уравнение адиабатического процесса.

Ответ: PV ^4/3 = const.

Не нашли, что искали? Воспользуйтесь поиском: