
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Упругой называется такая деформация, которая полностью исчезает после прекращения действия внешних сил.
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ИЗ РАСТЯЖЕНИЯ
Краткая теория
Изменение размеров или формы твердого тела под воздействием внешних сил называется деформацией.
Деформации всех видов делятся на пластические и упругие.
Упругой называется такая деформация, которая полностью исчезает после прекращения действия внешних сил.
Если после прекращения действия внешних сил упругие силы не могут восстановить первоначальную форму и размеры тела, то такая деформация называется пластической.
Пластические деформации имеют большое значение в технологии: штамповка, ковка, изгиб изделий возможны благодаря пластическим деформациям.
Английский ученый Роберт Гук в 18 веке обнаружил, что механическое напряжение, возникающее в упруго деформированном теле пропорционально его относительной деформации (закон Гука).
Для деформации растяжения закон Гука имеет вид:
 (1.1)
(1.1)
где:  – напряжение – физическая величина, численно равная упругой силе, приходящейся на единицу площади поперечного сечения образца.
– напряжение – физическая величина, численно равная упругой силе, приходящейся на единицу площади поперечного сечения образца.
 – относительное удлинение, которое показывает, на сколько увеличилась каждая единица первоначальной длины тела L0.
– относительное удлинение, которое показывает, на сколько увеличилась каждая единица первоначальной длины тела L0.
D L = L – L 0 – абсолютное удлинение образца,
L 0 – первоначальная длина образца,
L - длина образца после растяжения,
Е – модуль упругости (модуль Юнга).
Из формулы (1.1) имеем:
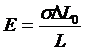 (1.2)
(1.2)
Если D L = L 0, то Е = s, т.е. физический смысл модуля Юнга состоит в том, что он равен нормальному напряжению, которое возникло бы в теле при увеличении его длины в два раза.
Размерность модуля Юнга в системе СИ:
[Е] = [s] =  = H/м2 = Па (1.3)
= H/м2 = Па (1.3)
С учетом того, что  формула 1.2. примет вид:
формула 1.2. примет вид:
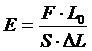 (1.4)
(1.4)
Напряжение sпроп. при котором нарушается пропорциональность между напряжение и относительной деформацией, называется пределом пропорциональности.
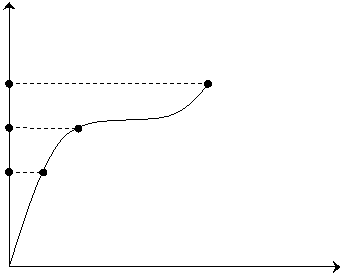
На графике (рис. 1) закон Гука выполняется на участке ОА. Точка «А» – соответствует пределу пропорциональности sпропор.
Пределом упругости называется наименьшее напряжение sупр. после снятия которого появляется остаточная деформация.
После предела упругости, напряжение растет медленнее, чем деформация и при некотором значении напряжения sпр тело разрушается. Это предел прочности. На графике это точка «С».
 s
s
s пр С
sупр В
sпроп
А

Рис. 1.1
Определить модуль упругости можно используя различные виды деформации. В нашей лаборатории используется деформация растяжения.
Оборудование.
1. Металлическая проволока верхним концом укреплена неподвижно. а на нижнем конце укреплен патрон с прямым стержнем, оканчивающийся платформой.
2. Микрометр с точностью измерения 0,01 мм укреплен вблизи нижнего конца проволоки на прямоугольном кронштейне (используется для измерения удлинения D L).
3. Грузы по 0,5 кг.
4. Микрометр для измерения диаметра проволоки.
Выполнение работы.
1. По наклеенной миллиметровой шкале измерить длину проволоки L0 между точками ее закрепления, в метрах с точностью до тысячных.
2. Измерить микрометром в нескольких местах диаметр проволоки d, определить
_
средний диаметр d, округляя его на порядок больше, чем отсчет по микрометру.
3. При отсутствии нагрузки F = 0 довести винт. укрепленного микрометра до соприкосновения с упором, пока засветится лампочка, и записать показания микрометра в таблицу 3.1.
4. Положить на платформу груз F = 0,5 кг, снова довести винт укрепленного микрометра до соприкосновения с упором, пока вспыхнет лампочка, и записать показания микрометра.
5. Увеличивая постепенно нагрузку на 0,5 кг, записывать показания микрометра. пока на платформе будет 2 кг.
6. Разгружают платформу, снимая по 0,5 кг, и записывая показания микрометра при разгрузке для 2 кг, 1,5 кг, 1 кг, 0,5 кг, 0 кг.
7. Для каждой нагрузки берут среднее значение из двух показаний микрометра при нагрузке и разгрузке.
8. Вычисляют удлинение проволоки D L для каждого из 4-х грузов по средним показаниям микрометра.
Таблица 3.1.
| № | L 0 (м) | d (м) | mi кг | показания микрометра | Среднее показание микрометра | D Li м | Еi Па | D Еi Па | (D Еi)2 Па | |
| при нагру- жении | при разгру-жении | |||||||||
| 0. | ||||||||||
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| 4. | ||||||||||

| S(D Еi)2 |
9. Вычисляют значение модуля Юнга в системе СИ для 0,5; 1,0; 1,5; 2 кг по формуле (3.2). Вывод расчетной формулы из формулы (1.4)
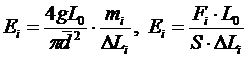 , так как
, так как  , g = 9,81 м/c2
, g = 9,81 м/c2 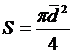 , то
, то
обозначим 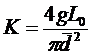 ;
;
 (3.2)
(3.2)
10.Находят среднее значение модуля Юнга Е:
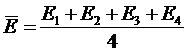 (3.3)
(3.3)
11.Находят отклонение каждого значения от среднего
 (3.4)
(3.4)
12.Вычисляют стандартное отклонение по формуле:
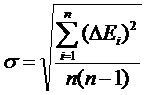 (3.5)
(3.5)
13. Вычисляют абсолютную ошибку по формуле
D E = a × s (3.6)
где коэффициент Стьюдента a = 3,2 и округляют D E.
14. Находят относительную ошибку
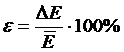 (3.7)
(3.7)
и записывают результат окончательно после округления
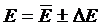
Контрольные вопросы.
1. Что называют деформацией?
2. Какие деформации считаются упругими, а какие пластическими?
3. Что называется механическим напряжением?
4. Закон Гука.
5. Что называется пределом пропорциональности, упругости, прочности?
6. Физический смысл модуля Юнга.
7. Вывести расчетную формулу из закона Гука.
Литература.
1. Грабовский Р.И. Курс физики. – М.: Высшая школа, 1980.
2. Зисман Г.А., Тодес О.М. Курс общей физики. – М.: Наука, 1972 – 1974, т.1.
3. Детлаф А.А. и др. Курс физики. – М.: Высшая школа, 1973 – 1979, т.1.
4. Савельев И.В. Курс общей физики – М.: Наука, 1977 – 1979, т.1.
ГЛОССАРИЙ
1) Абсолютная деформация – изменение размера тела по сравнению с первоначальным под действием приложенной силы
2) Относительная деформация – отношение абсолютного удлинения к первоначальной длине
3) Механическое напряжение – физическая величина, равная отношению действующей силы на деформируемое тело силы к площади поперечного сечения тела (образца)
4) Модуль упругости – (модуль Юнга)- постоянная для данного материала величина, характеризующая его упругие свойства. Измеряется в Паскалях
5) 1Паскаль – (сокращ. Па) – отношение силы в 1 Ньютон к площади поперечного сечения образца 1 м2 (в системе СИ)
6) Диаграмма растяжения - график зависимости механического напряжения от относительной деформации
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Теоретическая часть. 3. Экспериментальная установка……….…………………………………8 |
Не нашли, что искали? Воспользуйтесь поиском: