Теоретическая часть. 2.1. Теплоемкость и коэффициент Пуассона

2.1. Теплоемкость и коэффициент Пуассона

Теплоемкостью тела называют количество теплоты, необходимое для повышения температуры тела на 1 К.

Следовательно, если телу сообщили количество теплоты d'Q и при этом его температура из­менилась на d Т, то теплоемкость тела определяется как

(2.1)

Для характеристики тепловых свойств веществ пользуются удельной (с) и молярной (С) теплоемкостями, определяемых как

и , (2.2)

где m – масса тела;

n – число молей вещества.

Согласно (2.2), удельная теплоемкость вещества равна коли­честву теплоты, необходимому для нагревания на 1 К единицы мас­сы, а молярная – одного моля этого вещества.

Теплоемкости С_m, с и С зависят как от природы вещества, так и от условий, в которых происходит его нагревание. Это не­посредственно следует из первого начала термодинамики

(2.3)

и связано с тем, что изменение внутренней энергии тела dU и совершаемая работа d’A независимы и определяются характером процесса, в котором участвует тело. С учетом того, что

, (2.4)

где dV – изменение объема тела,

P – давление, из (2.2) и (2.3) следует, что, например, молярная теплоемкость физически однородного вещества определяется соотношением

. (2.5)

Величина характеризует изменение объема тела при изменении его температуры и в зависимости от характера происходящего с телом процесса может принимать любое значение от минус бесконечности до плюс бесконечности. То есть молярная теплоемкость (как и удельная) в зависимости от вида процесса может быть и положительной, и отрицательной, и иметь любое значение. Однако в конкретном процессе молярная теплоемкость имеет строго определенное значение и является однозначной характеристикой тепловых свойств вещества тела. Важнейшими являются молярные теплоемкости при постоянном объеме и при постоянном давлении. Именно они приводятся в таблицах справочных данных. Для любых твердых и жидких веществ различие между этими теплоемкостями не очень значительно ввиду малого объемного расширения этих веществ при изменении их температуры, а для газов оно является существенным.

Обратимся к молярным теплоемкостям идеального газа при постоянном объеме и при постоянном давлении. Внутренняя энергия идеального газа – это энергия теплового движения молекул и атомов в молекулах. Она складывается из кинетических энергий поступательного и вращательного движения молекул и энергии колебаний атомов в них. Согласно закону равнораспределения энергии по степеням свободы молекулы, на каждую поступательную и вращательную степень свободы приходится в среднем энергия, равная , где k – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Следовательно, средняя энергия теплового движения молекулы идеального газа равна

, (2.6)

где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы.

Внутренняя энергия n молей газа равна

, (2.7)

где N_A – число Авогадро;

R – универсальная газовая постоянная.

Внутренняя энергия идеального газа зависит только от его количества и абсолютной температуры и не зависит от объема, что является естественным следствием модели идеального газа, в которой потенциальной энергией межмолекулярного взаимодействия пренебрегают. В соответствии с (2.5) и (2.7) молярная теплоемкость идеального газа при постоянном объеме равна

. (2.8)

Из уравнения состояния идеального газа имеем:

. (2.9)

При постоянном давлении

. (2.10)

Значит, молярная теплоемкость идеального газа при постоянном давлении, как это следует из (2.5) с учетом (2.8) и (2.10), равна:

. (2.11)

Отношение теплоемкостей газа при постоянном давлении и постоянном объеме

(2.12)

называется коэффициентом Пуассона. Его значение определяется только числом степеней свободы молекул газа.

2.2. Взаимосвязь коэффициента Пуассона газа со скоростью распространения в нем звуковых волн.

Продольные волны в сплошной среде распространяются со скоростью

, (2.13)

где = – коэффициент сжимаемости среды;

r – ее плотность.

При распространении звуковых волн в газе любая небольшая его часть периодически сжимается и разжимается. В местах сжатия газ нагревается, а в местах разрежения – охлаждается. Вследствие малой теплопроводности газа и достаточно быстрой смены сжатия и разрежения (например, даже при относительно небольшой частоте звуковых колебаний 1000Гц эта смена происходит за тысячную долю секунды) любой объем газа можно считать теплоизолированным от остальной его части. В таком случае процесс изменения состояния газа в этом объеме при распространении звука можно считать адиабатическим, и, значит, подчиняющимся закону Пуассона:

(2.14)

Дифференцируя это уравнение по P

, (2.15)

находим производную объема по давлению:

(2.16)

Для коэффициента адиабатической сжимаемости получаем

= , (2.17)

а для скорости звука

. (2.18)

Из уравнения Менделеева-Клайперона следует, что

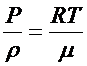, (2.19)

где m – молярная масса газа.

С учетом (2.19) и (2.18) получаем

(2.20)

Таким образом, измерив температуру газа и скорость распространения в нем звука, значение коэффициента Пуассона для этого газа можно рассчитать с помощью формулы (2.20).

2.3. Измерение скорости звука

В настоящей работе измерение скорости звука в воздухе основано на свойствах стоячих волн. Такие волны можно получить внутри наполненной воздухом трубы, если закрыть ее концы и на одном из торцов поместить источник звуковых колебаний. Стоячая волна в трубе образуется при сложении волны, идущей от источника, с волной, отраженной от противоположного торца трубы. Максимальное усиление звука в трубе будет в том случае, когда расстояние между торцами трубы (длина воздушного столба) будет равно целому числу длин полуволн:

, (2.21)

где n = 1, 2, 3 …;

l_n – длина воздушного столба, соответствующего данному номеру n;

l – длина звуковой волны.

Выражая длину волны через частоту колебаний f и скорость распространения , получаем:

(2.22)

При фиксированной частоте максимальная громкость звука достигается изменением расстояния между торцами трубы так, чтобы оно удовлетворяло условию (2.22). При этом на экране осциллографа можно наблюдать резкое увеличение амплитуды колебаний, регистрируемых с помощью установленного в трубе микрофона.

В соответствии с формулой (2.22), графиком зависимости l_n(n) должна быть прямая линия, тангенс угла наклона j которой равен

, (2.23)

где n₁ и n₂ – целые числа, а

и – соответствующие расстояния между торцами трубы при образовании в ней стоячей волны.

Таким образом, при известной частоте колебаний волны имея график зависимости l_n(n) через тангенс угла его наклона можно рассчитать скорость звука:

(2.24)

Не нашли, что искали? Воспользуйтесь поиском: