
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Закон Био-Савара-Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими физиками Ж.Био и Ф.Саваром, а результаты их исследований обобщил математик Лаплас. Закон Био-Савара-Лапласа для проводника с током  , элемент
, элемент  которого создает в некоторой точке А индукцию поля
которого создает в некоторой точке А индукцию поля  , записывается в виде (рис.4.2):
, записывается в виде (рис.4.2):

 ,
,
где  – вектор, по модулю равный длине
– вектор, по модулю равный длине  элемента проводника и совпадающий по направлению с током,
элемента проводника и совпадающий по направлению с током,  – радиус-вектор, проведенный из элемента
– радиус-вектор, проведенный из элемента  проводника в точку А поля,
проводника в точку А поля, 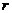 – модуль радиуса-вектора
– модуль радиуса-вектора  .
.
Модуль вектора  определяется выражением:
определяется выражением:
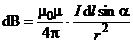 ,
,
где  – угол между векторами
– угол между векторами  и
и  .
.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: вектормагнитной индукции результирующего поля, создаваемого несколькими токами, равен векторной сумме магнитных индукций, создаваемых каждым током отдельно в данной точке поля:
 ,
,
где 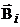 – магнитная индукция в данной точке поля, создаваемая каждым движущимся зарядом или током в отдельности.
– магнитная индукция в данной точке поля, создаваемая каждым движущимся зарядом или током в отдельности.
 1. Магнитное поле прямого тока – тока, текущего по тонкому прямому проводнику бесконечной длины. В произвольной т. А, удаленной от оси проводника на расстояние
1. Магнитное поле прямого тока – тока, текущего по тонкому прямому проводнику бесконечной длины. В произвольной т. А, удаленной от оси проводника на расстояние  , векторы
, векторы  от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа «к нам» (рис. 4.3). Поэтому сложение векторов можно заменить сложением их модулей
от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа «к нам» (рис. 4.3). Поэтому сложение векторов можно заменить сложением их модулей
 .
.
Заменим постоянную интегрирования  на угол
на угол 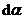 и выразим через него величины r и
и выразим через него величины r и  получим:
получим: 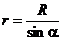 и
и 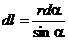 . Подставим эти выражения в формулу магнитной индукции, получим
. Подставим эти выражения в формулу магнитной индукции, получим 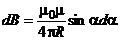 . Так как угол α для всех элементов прямого тока меняется от 0 до π, то магнитная индукция
. Так как угол α для всех элементов прямого тока меняется от 0 до π, то магнитная индукция
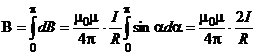 .
.
Следовательно, магнитная индукция поля прямого тока
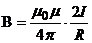 .
.
2. Магнитное поле в центре кругового проводника с током
 Все элементы проводника с током создают в центре витка магнитное поле одного направления, поэтому сложение векторов
Все элементы проводника с током создают в центре витка магнитное поле одного направления, поэтому сложение векторов  можно заменить сложением их модулей (рис.4.4), здесь sin α = 1, т.к. α = 900 и r = R =const, получим:
можно заменить сложением их модулей (рис.4.4), здесь sin α = 1, т.к. α = 900 и r = R =const, получим:

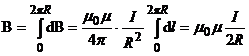 .
.
Магнитная индукция в центре витка равна
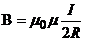 .
.
 4.3. Закон Ампера
4.3. Закон Ампера
Обобщая результаты исследования действия магнитного поля на проводники с током, А.Ампер установил, что сила 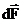 , с которой магнитное поле действует на элемент проводника
, с которой магнитное поле действует на элемент проводника  с током, находящийся в магнитном поле, равна
с током, находящийся в магнитном поле, равна
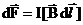 ,
,
где  – вектор, по модулю равный
– вектор, по модулю равный  и совпадающий по направлению с током. Модуль силы Ампера
и совпадающий по направлению с током. Модуль силы Ампера 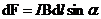 , где
, где  – угол между векторами
– угол между векторами  и
и  . Направление действия силы Ампера определяется по правилу левой руки (рис. 4.5): если вектор
. Направление действия силы Ампера определяется по правилу левой руки (рис. 4.5): если вектор  входит в ладонь, четыре вытянутых пальца совпадают с направлением тока, то большой отогнутый палец покажет направление силы, действующей на проводник с током.
входит в ладонь, четыре вытянутых пальца совпадают с направлением тока, то большой отогнутый палец покажет направление силы, действующей на проводник с током.
Законы Ампера и Био-Савара-Лапласа применяется для определения силы взаимодействия двух параллельных проводников с током. Два параллельных проводника с током притягиваются друг к другу, если направление тока одинаковое и отталкиваются, если токи текут в противоположных направлениях.
Сила Лоренца
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд 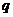 , движущийся в магнитном поле со скоростью
, движущийся в магнитном поле со скоростью 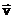 , называется силой Лоренца и выражается формулой:
, называется силой Лоренца и выражается формулой:
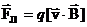 ,
,
где  – индукция магнитного поля. Модуль силы Лоренца определяется по формуле
– индукция магнитного поля. Модуль силы Лоренца определяется по формуле 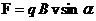 , где α – угол между векторами магнитной индукции и скорости. Направление силы Лоренца определяется по правилу левой руки: если левую руку расположить так чтобы вектор
, где α – угол между векторами магнитной индукции и скорости. Направление силы Лоренца определяется по правилу левой руки: если левую руку расположить так чтобы вектор  входил в ладонь, четыре вытянутых пальца направить вдоль вектора
входил в ладонь, четыре вытянутых пальца направить вдоль вектора 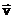 , то отогнутый большой палец покажет направление силы Лоренца, действующей на положительный заряд, для отрицательного заряда направление силы противоположное. Сила Лоренца направлена перпендикулярно скорости, поэтому она изменяет только направление скорости и работы не совершает.
, то отогнутый большой палец покажет направление силы Лоренца, действующей на положительный заряд, для отрицательного заряда направление силы противоположное. Сила Лоренца направлена перпендикулярно скорости, поэтому она изменяет только направление скорости и работы не совершает.
Если на движущийся электрический заряд помимо магнитного поля действует еще электрическое поле, то результирующая сила
 .
.
Это выражение называется формулой Лоренца.
Если заряженная частица движется в магнитном поле со скоростью 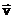 , перпендикулярной вектору
, перпендикулярной вектору  , то сила Лоренца постоянна по модулю, нормальна к траектории движения и, являясь центростремительной силой, заставляет частицу двигаться по окружности радиуса
, то сила Лоренца постоянна по модулю, нормальна к траектории движения и, являясь центростремительной силой, заставляет частицу двигаться по окружности радиуса 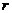 :
:  .
.
Период вращения частицы, т.е. время, за которое частица совершает один оборот:
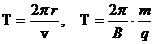 .
.
 4.5. Поток магнитной индукции
4.5. Поток магнитной индукции
Потоком вектора магнитной индукции (магнитным потоком) через площадку  называется скалярная величина, равная
называется скалярная величина, равная
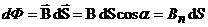 ,
,
где  – проекция вектора
– проекция вектора  на направление нормали к площадке
на направление нормали к площадке  (
( – угол между векторами
– угол между векторами  и
и  );
);  – вектор, модуль которого равен
– вектор, модуль которого равен  , а направление совпадает с направлением нормали
, а направление совпадает с направлением нормали  к площадке (рис.4.6).
к площадке (рис.4.6).
Общий поток магнитной индукции через произвольную поверхность равен 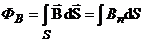 .
.
Для однородного поля и плоской поверхности  .
.
Единица магнитного потока – вебер (Вб) [1 Вб=1 Тл·м2].
Не нашли, что искали? Воспользуйтесь поиском: