ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. По проводу, согнутому в виде квадрата со стороной 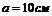, течет ток силой . Найти магнитную индукцию В в точке О пересечения диагоналей квадрата.

Дано: .

Найти: В?

Решение: Расположим квадратный виток в плоскости чертежа. Согласно принципу суперпозиции магнитных полей, (1), где – магнитные индукции полей, создаваемых токами, протекающими по каждой стороне квадрата.

В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка "к нам". Кроме того, из соображений симметрии следует, что модули этих векторов одинаковы: В ₁ = В ₂ = В ₃ = В ₄. Это позволяет векторное равенство (1) заменить скалярным: В = 4 В ₁. (2)

Магнитная индукция поля, создаваемого отрезком прямолинейного провода с током, выражается формулой . (3)

Учитывая, что и , формулу (3) можно переписать в виде: .

Подставив выражение (3) в формулу (2), найдем .

Как видно из рисунка, и (так как ). Тогда .

Проверим, дает ли расчетная формула единицу магнитной индукции. Для этого в правую часть формулы вместо символов величин подставим обозначения их единиц:

Найденная единица является единицей магнитной индукции. Произведем вычисления:

Пример 2. Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой , расположены на расстоянии друг от друга. Определить магнитную индукцию В поля, создаваемого проводниками с током в точке А (см. рис.), отстоящей от оси одного проводника на расстоянии и от другого – на расстоянии .

Дано: ; ; ; .

Найти: В?

Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направление магнитных индукций В ₁ и В ₂ полей, создаваемых проводником в отдельности, и сложим их геометрически:

Модуль вектора может быть найден по теореме косинусов:

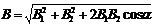, (1), где – угол между векторами и .

Значения магнитных индукций В ₁ и В ₂ выражаются через силу тока I и, соответственно, расстояния и от проводов до точки А: ;

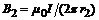
Подставив выражения В ₁ и В ₂ в формулу (1) и вынеся за знак корня, получим

. (2)

Вычислим . Из рисунка видно, что

равен DAC (как углы с соответственно перпендикулярными сторонами). По теореме косинусов запишем , где d – расстояние между проводами. Отсюда

.

Подставив в формулу (2) значения , определим искомую индукцию:

Пример 3. По двум длинным параллельным проводникам (фидерам) текут токи в одном направлении силой . В одной плоскости с фидерами параллельно им закреплен отрезок замкнутого прямого проводника длиной . Определить силу тока, протекающего по проводнику, если после снятия закреплений он начинает двигаться с ускорением . Масса проводника , он расположен на расстоянии от одного и на расстоянии от другого фидера. Принять фидеры и проводник за линейные и находящиеся в воздухе (см. рис.).

Дано: ;

; ; ;

; .

Найти: I?

Решение. На рисунке показано сечение, перпендикулярное проводникам. Ток в фидерах 1 и 2 создает магнитное поле, в котором находится отрезок замкнутого прямого проводника 3. На элемент проводника с током I в магнитном поле действует сила Ампера

,

где В – индукция поля. Угол под знаком синуса составлен направлениями вектора индукции и элемента проводника с током. По условию задачи индукция одинакова для всех точек отрезка проводника и проводник длиной прямой. Сила Ампера . (1).

Найдем индукцию в той области поля, где расположен отрезок проводника. Определим ее, используя закон Био-Савара-Лапласа для бесконечно длинных прямолинейных проводников: , , где – магнитная проницаемость среды; – магнитная постоянная; I – сила тока в фидерах, создающая на расстоянии r индукцию В.

Вектор индукции перпендикулярен плоскости, содержащей r и элемент тока I. Его направление определяется правилом винта. По условию задачи вектор В лежит в плоскости, перпендикулярной проводникам, и направлен под прямым углом к r. Поэтому фидеры в области отрезка проводника создают поля, векторы индукции которых имеют одинаковое направление. Следовательно, суммарная индукция , или . (2)

Подставив выражение (2) в (1), найдем силу, действующую на отрезок проводника с током I ₃: . (3)

Направление силы F определяется правилом левой руки. Если ток I ₃ противоположен токам I ₁ и I ₂, это будет сила отталкивания, когда ток I ₃ совпадет с направлением токов I ₁ и I ₂, возникает сила притяжения. По условию задачи и , поэтому уравнение (3) можно записать в виде . (4)

Подставив во второй закон Ньютона силу, найденную по формуле (4), можно определить искомый ток:

.

Пример 4. Плоский квадратный контур со стороной 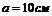, по которому течет ток , свободно установился в однородном магнитном поле . Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) ; 2) . При повороте контура сила тока в нем поддерживается неизменной.

Дано: ; ; ;

; ;

Найти: А ₁, А ₂?

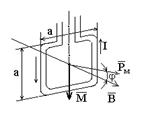Решение: Задачу можно решить следующим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур:

; ; ,

где Ф ₁ – магнитный поток, пронизывающий контур до перемещения; Ф ₂ – магнитный поток после перемещения.

, ,

, .

Пример 5. Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле напряженностью Н = 10³ А/м. Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Дано: U = 400 В; Н = 10³ А/м; е = 1,6^.10^-19Кл; m = 9,1^.10^-31кг.

Найти: R, n -?

Решение. Радиус кривизны траектории электрона определим исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение: F_л = ma_n, или

, (1)

где е – заряд электрона; V – скорость электрона; В – магнитная индукция; m – масса электрона; R – радиус кривизны траектории; α – угол между направлением вектора скорости и вектором (в данном случае _┴ , α = 90^о, (sin α= 1).

Из формулы (1) найдем . (2)

Входящий в равенство (2) импульс mV может быть выражен через кинетическую знергию W электрона: . (3)

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством: W = e U.

Подставив это выражение W в формулу (3), получим . Магнитная индукция В может быть выражена через напряженность Н магнитного поля в вакууме соотношением В = μ₀ Н (где μ₀ - магнитная постоянная).

Подставив найденные выражения В и mV в формулу (2), определим

. (4)

Подставим значения в формулу (4) и произведем вычисления:

.

Для определения частоты обращения n воспользуемся формулой, связывающей частоту со скоростью и радиусом: (5)

Подставив в формулу (5) выражение (2), получим: , или .

Все величины, входящие в эту формулу, ранее были выражены в системе СИ. Подставим их и произведем вычисления:

.

Пример 6. В однородном магнитном поле (В = 0,1 Тл) равномерно с частотой n = 10 с^-1 вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь S рамки равна 150 см². Определить мгновенное значение э.д.с. индукции, соответствующее углу поворота рамки φ = 30^о.

Дано: В = 0,1 Тл; n = 10 с^-1; N = 1000 витков; S = 150см²= 0,015м²; φ = 30^о.

Найти: E _i -?

Решение: Мгновенное значение э.д.с. индукции Е _i определяется основным уравнением электромагнитной индукции Фарадея-Максвелла: (1), где Ф_i – сцепление. Магнитный поток Ф_i, пронизывающий 1 виток и число витков N, плотно прилегающих друг к другу, связаны соотношением Ф = N Ф _i (2)

Подставив выражение (2) в формулу (1), получим (3)

При вращении рамки (см. рис.) магнитный поток Ф, пронизывающий рамку в момент времени t, определяется соотношением Ф_i = В S cos ωt, где В – магнитная индукция; S – площадь рамки; ω – круговая (или циклическая) частота.

Подставив в формулу (2) выражение Ф и продифференцировав полученное выражение по времени, найдем мгновенное значение э.д.с. индукции: E _i = N B S ω sin ω.t (4)

Круговая частота ω связана с частотой вращения n соотношением ω = 2π n. Подставив выражение ω в формулу (3) и заменив ωt на φ, получим E _i = 2π n N B S·sin φ. Произведем вычисления: E _i = 2·3,14·10·10³ ·0,1·1,5·10^-2·0,5 В = 47,1 В.

Пример 7. По длинному соленоиду с немагнитным сердечником сечением S = 5,0 см², содержащему N = 1200 витков, течет ток силой I = 2 А. Индукция магнитного поля в центре соленоида В = 10,0 мТл. Определить его индуктивность.

Дано: S = 5,0 см² = 5^.10^-4м²; N = 1200 витков; I = 2 А; В = 10,0 мТл.

Найти: L?

Решение: Задачу можно решить, исходя из общего определения индуктивности контура как коэффициента пропорциональности между током I в контуре и собственным магнитным потоком Ф сквозь него:

Ф = L·I. (2)

Поскольку , полный поток равен Ф = NBS. Подставив это значение в (2), найдем индуктивность соленоида.

КОНТРОЛЬНАЯ РАБОТА 4

1. По двум длинным параллельным проводам, расстояние между которыми d=5 см, текут одинаковые токи I=70 А. Определить индукцию В и напряженность Н магнитного поля в точке, удаленной от каждого провода на расстояние r= 5 см, если токи текут: а) в одинаковом, б) в противоположных направлениях.

2. Два бесконечно длинных прямых проводника скрещены под прямым углом. По проводникам текут токи силой I₁=100 А и I₂=50А. Pасстояние между проводниками d=20 см. Определить индукцию магнитного поля в точке, лежащей на середине общего перпендикуляра к проводникам.

3. Ток силой I=50 А течет по проводнику, согнутому под прямым углом. Найти напряженность H магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии в=20 см. Считать, что оба конца проводника находятся очень далеко от вершины угла.

4. По проводнику, изогнутому в виде окружности, течет ток. Напряженность магнитного поля в центре окружности Н₁=50 А/м. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определить напряженность H₂ магнитного поля в точке пересечения диагоналей этого квадрата.

5. По двум одинаковым круговым виткам радиусом R=6 см, плоскости которых взаимно перпендикулярны, а центры совпадают, текут одинаковые токи силой I=3 А. Найти индукцию магнитного поля в центре витков.

6. Прямолинейный проводник расположен перпендикулярно плoскости кругового проводника радиусом 20 см и проходит на расстоянии половины радиуса от центра. Прямолинейный ток имеет силу 9,42 А, а круговой - 2 А. Определить напряженность магнитного поля, создаваемого токами в центре круга.

7. Прямой проводник изогнут в виде угла, равного 60°. По проводнику течет ток силой 10 А. Определить индукцию магнитного поля при μ=1 на биссектрисе внутри угла на расстоянии 20 см от вершины.

8. В однородном магнитном поле с индукцией В=0,5Тл находится прямоугольная рамка длиной а=8см и шириной b=5см, содержащая N=100 витков тонкой проволоки. Ток в рамке I = 1А, а плоскость рамки параллельна линиям магнитной индукции. Определить: 1) магнитный момент рамки; 2) вращающий момент, действующий на рамку.

9. В однородном магнитном поле с индукцией В=1Тл находится квадратная рамка со стороной а=10см, по которой течет ток I = 4А. плоскость рамки перпендикулярна линиям магнитной индукции. Определить работу А, которую необходимо затратить для поворота рамки относительно оси, проходящей через середину ее противоположных сторон: 1) на 90⁰; 2) на 180⁰; 3) на 360⁰.

10. Два длинных прямолинейных проводника 1 и 2 расположены параллельно на расстоянии ВС = 2см друг от друга (см. рис.). Токи в проводниках направлены в противоположные стороны, при этом каждый из проводников на расстоянии 1см от себя создает магнитное поле с индукцией, по модулю равной В=1^.10^-4 Тл. Чему равен модуль вектора индукции магнитного поля в точке А (ВА=АС)?

11. Определить магнитную индукцию на оси тонкого проволочного кольца радиусом R = 5см, по которому течет ток I = 10А, в точке А, расположенной на расстоянии d = 10см от центра кольца.

12. Напряженность Н магнитного поля в центре кругового витка с магнитным моментом р_m=1,5 А^.м² равна 150 А/м. определить: 1) радиус витка; 2) силу тока в витке.

13. По тонкому стержню длиной l=40 см равномерно распределен заряд q=500 нКл. Стержень приведен во вращение с постоянной угловой скоростью ω=20 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Определить: 1) магнитный момент p_м, обусловленный вращением заряженного стержня; 2) отношение магнитного момента к моменту импульса, если стержень имеет массу m=10 г.

14. Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности радиусом R=0,53·10^{-8 см. Вычислить магнитный момент} p_m эквивалентного кругового тока и механический момент М, действующий на круговой ток, если атом помещен в магнитное поле с индукцией В=0,4 Тл, направленной параллельно плоскости орбиты электрона.

15. В однородном магнитном поле с индукцией В=0,2 Тл находится прямой проводник длиной l = 15см, по которому течет ток I = 5А. На проводник действует сила F =0,13Н. Определить угол α между направлениями тока и вектором магнитной индукции.

16. Электрон, ускоренный разностью потенциалов U=0,5кВ, движется параллельно прямолинейному длинному проводнику на расстоянии r = 1см от него. Определить силу, действующую на электрон, если через проводник пропускать ток I=10А.

17. Электрон, влетев в однородное магнитное поле с магнитной индукцией В=2 мТл, движется по круговой орбите радиусом R= 15см. Определить момент р_m эквивалентного кругового тока.

18. На сколько отличаются наибольшее и наименьшее значения модуля силы, действующей на прямой провод длиной 20см с током 10А, при различных положениях провода в однородном магнитном поле, индукция которого равна 1Тл?

19. По плоской круглой рамке, имеющей 20 витков радиусом 2 см течет ток в 1 А. Нормаль к рамке составляет угол 90° с направлением магнитного поля напряженностью 30 А/м (воздух). Найти изменение вращающего момента, действующего на рамку, если из 20 витков рамки сделать один круглый виток.

20. Индукция магнитного поля изменяется в зависимости от времени так, как показано на графике. Линии индукции этого однородного поля перпендикулярны плоскости проволочного кольца площадью . Чему равно максимальное значение индуцируемой в кольце э.д.с.?

21. Как будут вести себя два проводника с токами, расположенные перпендикулярно друг другу?

22. По двум параллельным проводникам длиной l=3 м каждый текут одинаковые токи силой I=500 А. Расстояние между проводниками d=10 см. Определить силу F взаимодействия проводников.

23. Если скорость заряженной частицы , влетевшей в однородное магнитное поле и начавшей двигаться по окружности с периодом обращения , увеличить в 3 раза, то период обращения станет равным…

24. Какой ток следует пропустить по проводнику, для того, чтобы сила, действующая со стороны однородного магнитного поля с индукцией 0,1 Тл на прямолинейный проводник длиной 4м, причем проводник расположен под углом 30⁰ к вектору индукции поля, была равна 1Н.

25. Прямой провод длиной l=40 см, по которому течет ток силой I=100 А, движется в однородном магнитном поле с индукцией В=0,5 Т. Какую работу А совершат силы, действующие на провод со стороны поля, переместив его на расстояние S=40 см, если направление перемещения перпендикулярно линиям индукции и проводу?

26. Проводник длиной 50 см, по которому течет ток силой 1 А, движется со скоростью 1,4 м/с перпендикулярно индукции магнитного поля напряженностью 20 А/м. Определить работу перемещения проводника за 1 ч движения.

27. Проводник длиной 0,6 м движется поступательно со скоростью 0,8 м/с в плоскости, перпендикулярной магнитному полю с индукцией 0,5 мТ. Разность потенциалов, приложенная к концам проводника U=100В. Bo сколько раз мощность, затраченная на нагревание проводника, больше мощности, затраченной на перемещение проводника в магнитном поле?

28. Прямолинейный проводник длиной 0,5м, по которому течет постоянный ток силой 20А, находится в однородном магнитном поле индукция которого В=0,25 Тл, и расположен перпендикулярно линиям магнитной индукции. Какая совершается работа при перемещении проводника на 0,1 метра по направлению действия силы Ампера?

29. В магнитном поле, индукция которого равна , вращается стержень длиной с постоянной угловой скоростью (см. рис.). Ось вращения перпендикулярна стержню, проходит через его конец О и параллельна линиям индукции магнитного поля. ЭДС индукции, возникающая в стержне, равна …

30. Виток радиусом R=25 см, по которому течет ток силой I= 45 А, свободно установился в однородном магнитном поле напряженностью Н=10³А/м. Bитoк повернули относительно диаметра на угол φ=30°.Определить совершенную работу А.

31. Проволочный контур в виде квадрата со стороной 10 см расположен в однородном магнитном поле так, что плоскость квадрата перпендикулярна линиям индукции магнитного поля. Индукция магнитного поля . На какой угол надо повернуть плоскость контура, чтобы изменение магнитного потока через контур составило ?

32. Чему равен радиус окружности, если кинетическая энергия протона, движущегося по окружности в однородном магнитном поле с индукцией В=1,5 Тл, равна 17,2^.10^-13Дж?

33. Протон и дейтрон (ядро изотопа водорода ²₁Н) влетают в однородное магнитное поле перпендикулярно линиям индукции. Как связаны между собой периоды Т₁ и Т₂ обращения по окружностям, соответственно, протона и дейтрона?

34. Параллельно пластинам плоского конденсатора создано однородное магнитное поле напряженностью 3200 А/м. Между пластинами перпендикулярно направлению вектора индукции и параллельно пластинам движется электрон со скоростью 5·10⁶ м/с. Определить напряженность электрического поля между пластинами.

35. Заряд движется в вакууме прямолинейно со скоростью 10⁵ м/с во взаимно перпендикулярных магнитном и электрическом полях. Каково должно быть отношение напряженностей этих полей, чтобы имело место такое движение? Как должна быть направлена скорость заряда?

36. Если два электрона с кинетическими энергиями К₁ и К₂ соответственно движутся по окружностям в однородном магнитном поле в плоскости, перпендикулярной линиям индукции поля, то чему равно отношение их периодов обращения Т₁/Т₂?

37. Электрон движется в однородном магнитном поле перпендикулярно линиям индукции. Определить силу F, действующую на электрон со стороны поля, если индукция поля B=0,2 Т, а радиус кривизны траектории R=0,2 см (см.рис.).

38. Заряженная частица движется по окружности в однородном магнитном поле с индукцией В=1 Тл. Период обращения равен Т= 3,4^.10^-11с. Чему равен удельный заряд частицы q / m?

39. Электрон движется по окружности радиуса 2см в однородном магнитном поле, имея импульс 6,4^.10^-23кг^.м/с. Найти индукцию поля.

40. Протон и дейтрон (ядро изотопа водорода ²₁Н) имеющие одинаковые кинетические энергии, влетают в однородное магнитное поле перпендикулярно линиям индукции. Как связаны между собой радиусы R₁ и R₂ окружностей, по которым, соответственно, движутся протон и дейтрон (массы протона и дейтрона считать равными)?

41. Проволочная рамка площадью 100см² помещена в однородное магнитное поле, зависимость индукции которого от времени показана на графике. Какова э.д.с. индукции в рамке в момент времени t=3с, если плоскость рамки составляет угол в 30⁰ с направлением линий магнитной индукции?

42. Катушка из 10 витков присоединена к амперметру так, что сопротивление всей цепи равно 100 Ом. Если при помещении катушки в равномерно изменяющееся однородное магнитное поле амперметр показывает ток 100 мА, как изменится магнитный поток через один виток катушки за 2с?

43. В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд q=10 мкКл. Определить изменение магнитного потока ΔФ через кольцо, если сопротивление цепи гальванометра r=30 Ом.

44. По проводнику с длиной активной части идет ток . Проводник помещен в магнитное поле с индукцией 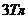, перпендикулярное направлению тока. Определить силу, действующую на проводник со стороны магнитного поля.

45.Рамка площадью S=200 см² равномерно вращается с частотой n=10с^-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (B=0,2 Т). Определить среднее значение э.д.с. индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения.

46.Тонкий медный проводник массой m=1 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (B=0,1 Т) так, что его плоскость перпендикулярна линиям поля. Определить заряд q, который протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию. Сторона квадрата а=10см.

47.B однородном магнитном поле напряженностью H=2000 А/м, равномерно с частотой n=10 с^-1 вращается стержень длиной l= 20 см так, что плоскость его вращения перпендикулярна линиям напряженности, а ось вращения проходит через один из его концов. Определить индуцируемую на концах стержня разность потенциалов.

48. В однородном магнитном поле, индукция которого равна 0,1 Тл, равномерно вращается катушка, состоящая из 100 витков проволоки. Площадь поперечного сечения катушки 100см². Ось вращения катушки перпендикулярна оси катушки и направлению магнитного поля. Угловая скорость вращения катушки равна 10 рад/с. Чему равна максимальная э.д.с., возникающая в катушке?

49. В однородном магнитном поле напряженностью 1000 А/м (в воздухе) равномерно вращается круглая рамка, имеющая 100 витков, радиус которых 6 см. Ось вращения проходит через диаметр рамки и перпендикулярна магнитному полю, сопротивление рамки 1 Ом, угловая скорость ее вращения 10 с^-1. Найти максимальную силу тока в рамке.

50. Круглая рамка, имеющая 200 витков и площадь 100 см², равномерно вращается в однородном магнитном поле с индукцией 0,03 Т вокруг оси, перпендикулярной полю и проходящей через ее диаметр. Вычислить частоту вращения, если максимальный ток, индуцируемый в рамке, при ее сопротивлении 20 Ом, составляет 0,02 А?

51. Соленоид сечением S=10 см² содержит N=1000 витков. Индукция B магнитного поля внутри соленоида при силе тока I=5 А равна 0,1 Т. Определить индуктивность L соленоида.

52. На картонный каркас длиной l=0,8 м и диаметром D=4 см намотан в один слой провод диаметром d=0,25 мм так, что витки плотно прилегают друг к другу. Вычислить индуктивность L получившегося соленоида.

53. Катушка, намотанная на немагнитный цилиндрический каркас, имеет N=250 витков и индуктивность L₁=36 мГн. Чтобы увеличить индуктивность катушки до L₂= 100 мГн, обмотку катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Сколько витков оказалось в катушке после перемотки?

54. Соленоид содержит N=600 витков. При силе тока I=10А магнитный поток Ф=80 мкВб. Определить индуктивность соленоида.

55. Соленоид содержит N=800 витков. Сечение сердечника (из немагнитного материала) S=10 см². По обмотке течет ток, создающий поле с индукцией B=8 мТ. Определить среднее значение э.д.с. (E_i) самоиндукции, которая возникает на зажимах соленоида, если сила тока уменьшается практически до нуля за время Δt = 0,8 мс.

56. По катушке индуктивностью L=8 мкГ течет ток силой I=6 А. При выключении тока его сила изменяется практически до нуля за время Δt=5 мс. Определить среднее значение э.д.с. < E_i > самоиндукции, возникающей в контуре.

57. Катушка длиной l=20см имеет N=400 витков. Площадь поперечного сечения катушки S=9см². Найти индуктивность L₁ катушки. Какова будет индуктивность L₂ катушки, если внутрь катушки введен железный сердечник? Магнитная проницаемость материала сердечника μ=400.

58. Соленоид имеет N=1000 витков, диаметр d=10 см и длину l=60 см. Сила тока в нем равномерно возрастает на ΔI=0,2 А за Δt=1 с. На соленоид надето кольцо из медной проволоки, имеющей площадь поперечного сечения S=2 мм². Найти силу индукционного тока, возникающего в кольце.

59. Проволочная рамка, имеющая форму равностороннего треугольника, помещена в однородное магнитное поле с индукцией В=0,06 Тл, направление линий которой составляет угол α = 30⁰ с перпендикуляром к плоскости рамки. При равномерном уменьшении индукции до нуля за время ∆t=0,03 с в рамке индуцируется э.д.с. 30мВ. Какова длина стороны рамки?

60. Сколько витков проволоки диаметром d=0,6мм имеет однослойная обмотка катушки, индуктивность которой L=1мГн и диаметр D=4 см? Витки плотно прилегают друг к другу.

61. Сколько витков имеет катушка, индуктивность которой L=1мГн, если при токе I=1А магнитный поток сквозь катушку Ф=2 мкВб?

62. Электрон, ускоренный разностью потенциалов , влетает в однородное магнитное поле, линии индукции которого перпендикулярны направлению его движения. Индукция магнитного поля 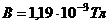. Радиус окружности, по которой будет двигаться электрон, равен

63. На линейный проводник длиной , расположенный перпендикулярно магнитному полю, действует сила , если ток в проводнике равен . Найдите индукцию магнитного поля.

64. Круговой контур радиусом r =2см помещен в однородное магнитное поле, индукция которого В=0,2 Тл. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R=1 Ом. Какое количество электричества q пройдет через катушку при повороте ее на угол α=90⁰.

65. Соленоид длиной l =50см и площадью поперечного сечения S=2см² имеет индуктивность L=0,2 мкГн. При каком токе I объемная плотность энергии магнитного поля внутри соленоида ω₀=1 мДж/м³?

66. В однородном магнитном поле с индукцией В=0,1 Тл движется проводник длиной l =10см. Скорость движения проводника v= 15 м/с и направлена перпендикулярно к магнитному полю. Найти индуцированную в проводнике э.д.с.

67. Соленоид содержит N=800 витков. При силе тока I=1А магнитный поток Ф=0,1 мВб. Определить энергию W магнитного поля соленоида. Сердечник выполнен из немагнитного материала, магнитное поле во всем объеме однородно.

68. В однородном магнитном поле, индукция которого В = 0,1Тл, равномерно вращается катушка, состоящая из N=100 витков проволоки. Частота вращения катушки n=5 с^-1; площадь поперечного сечения катушки S=0,01 м². Ось вращения перпендикулярна к оси катушки и направлению магнитного поля. Найти максимальную э.д.с. индукции во вращающейся катушке.

69. В магнитном поле, индукция которого В = 0,05 Тл, вращается стержень длиной l =1м с угловой скоростью ω=20 рад/с. Ось вращения проходит через конец стержня и параллельна магнитному полю. Найти э.д.с. индукции, возникшую на концах стержня.

70. В магнитном поле, индукция которого В=0,1 Тл, помещена квадратная рамка из медной проволоки. Площадь поперечного сечения проволоки s=1 мм², площадь рамки S=25 см². Нормаль к плоскости рамки параллельна магнитному полю. Какое количество электричества q пройдет по контуру рамки при исчезновении магнитного поля?

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

Закон Кулона
Напряженность электрического поля	;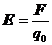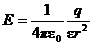
Принцип суперпозиции
Поток вектора напряженности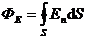
Поверхностная плотность заряда
Теорема Гаусса для электрического поля в вакууме
Напряженность поля равномерной бесконечной плоскости
Напряженность поля двух бесконечных равномерно заряженных плоскостей
Напряженность поля заряженной сферической поверхности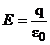
Циркуляция вектора напряженности
Потенциал электростатичес­кого поля
Разность потенциалов	Δ φ = (φ 1 – φ 2) = .
Электроемкость уединенного проводника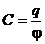
Электроемкость шара	С = 4pεε0 R.
Емкость плоского конденсатора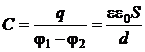
Электрическая емкость параллельно соединенных конденсаторов
Электрическая емкость последовательно соединенных конденсаторов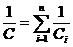
Энергия заряженного уединенного проводника
Энергия заряженного плоского конденсатора
Энергия электростатического поля
Объемная плотность энергии	ω = W / V: .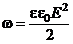
Поляризованность диэлектрика	; æ
Связь между диэлектрической проницаемостью и диэлектрической восприимчивастью вещества	æ
Cила тока
Плотность тока
Электродвижущая сила
Сопротивление проводника
Закон Омадля однородного участка цепи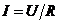
Закон Ома в дифференциальной форме
Закон Ома для замкнутой цепи
Общее сопротивление при последовательном соединении сопротивлений
Общее сопротивление при параллельном соединении сопротивлений
Закона Джоуля-Ленца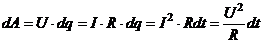
Закона Джоуля-Ленца в дифференциальной форме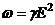
Мощность тока
Правила Кирхгофа	;
Связь между индукцией и напряженностью магнитного поля
Закон Био-Савара-Лапласа
Магнитная индукция поля прямого тока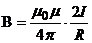
Магнитная индукция в центре кругового проводника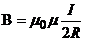
Закон Ампера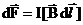
Сила Лоренца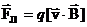
Формулой Лоренца
Поток магнитной индукции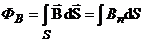
Работа по перемещению проводника с током в магнитном поле
Закон электромагнитной индукции Фарадея
Э.д.с. самоиндукции
Энергия магнитного поля

СПИСОК ЛИТЕРАТУРЫ

1. Трофимова Т.И. Курс физики: учеб. пособие / Т.И. Трофимова. – 6-е изд., стереотип. – М.: Высная школа, 1999. – 542с.

2. Савельев, И.В. Курс общей физики: учеб. пособие: в 3 т. Т.2 /И.В.Савельев. – 2-е изд., перераб. – М.: Наука, 1982. – 432с.

3.Детлаф А.А. Курс физики: учеб. пособие / А.А. Детлаф, Б.М. Яворский. – 3-е изд., исправл. – М.: Высная школа, 2001. – 718с.

4. Поливанов М.А. Электричество и магнетизм: учеб. пособие / М.А. Поливанов [и др.]. – Казань: Изд-во Казан. гос.технол.ун-та., 2007. -164 с.

Не нашли, что искали? Воспользуйтесь поиском: