
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Политропный процесс и его обобщающее значение
Опыт показывает, что отдельные процессы, происходящие в тепловых машинах, нередко полностью или частично с достаточной точностью описываются уравнением вида
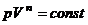 , (6.50)
, (6.50)
В принципе любой произвольный процесс можно описать в  - координатах (по крайней мере, на небольшом участке) этим уравнением, подбирая соответствующие значения
- координатах (по крайней мере, на небольшом участке) этим уравнением, подбирая соответствующие значения  . Процесс, описываемый уравнением (6.50), называется политропным, а кривую процесса называют политропой. Политропы - это кривые, описывающие процессы в газах, в которых происходят изменения всех термодинамических параметров. Показатель политропы
. Процесс, описываемый уравнением (6.50), называется политропным, а кривую процесса называют политропой. Политропы - это кривые, описывающие процессы в газах, в которых происходят изменения всех термодинамических параметров. Показатель политропы  может принимать любое численное значение от 1 до
может принимать любое численное значение от 1 до  , но для данного процесса он является величиной постоянной.
, но для данного процесса он является величиной постоянной.
Из уравнения (6.50) и уравнение Клайперона – Менделеева для идеальных газов  получим связь между параметрами состояния газа
получим связь между параметрами состояния газа  ,
,  и
и  в любых двух точках на политропе
в любых двух точках на политропе
 ,
,  ,
,  (6.51)
(6.51)
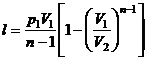 или
или  (6.52)
(6.52)
 , (6.53)
, (6.53)
 , (6.54)
, (6.54)
 .(6.55)
.(6.55)

 (6.56)
(6.56)
 представляет собой теплоёмкость идеального газа в политропном процессе, а показатель политропы определяется соотношением
представляет собой теплоёмкость идеального газа в политропном процессе, а показатель политропы определяется соотношением
 . (6.57)
. (6.57)
 (6.60)
(6.60)
Политропный процесс является обобщающим по отношению к основным обратимым термодинамическим процессам с идеальным газом. Рассмотренные выше термодинамические процессы представляют собой частные случаи политропного процесса. Действительно, если в формулу (6.50) подставить значения  , соответствующие частным термодинамическим процессам, то будем получать значения теплоёмкостей этих процессов.
, соответствующие частным термодинамическим процессам, то будем получать значения теплоёмкостей этих процессов.
Так:
при  (изобарный процесс)
(изобарный процесс) 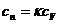 или
или  ;
;
при 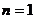 (изотермический процесс)
(изотермический процесс)  ;
;
при  (изохорный процесс)
(изохорный процесс)  ;
;
при  (адиабатный процесс)
(адиабатный процесс)  .
.
Не нашли, что искали? Воспользуйтесь поиском: