
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Прототипы задания В-11 из ЕГЭ 2012
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
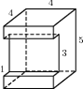
|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

|
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
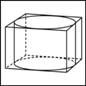
|
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
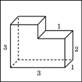
|
В цилиндрический сосуд налили  воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  . .

|
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.

|
В сосуд, имеющий форму правильной треугольной призмы, налили 2300  воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в  . .
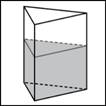
|
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает  см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в  раза больше, чем у первого? Ответ выразите в см. раза больше, чем у первого? Ответ выразите в см.

|
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы. . Найдите объем цилиндра, описанного около этой призмы.

|
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы. . Найдите объем цилиндра, описанного около этой призмы.
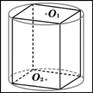
|
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

|
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

|
| Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах. |
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

|
Площадь поверхности куба равна 18. Найдите его диагональ.

|
Объем куба равен 8. Найдите площадь его поверхности.

|
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.

|
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на  . .
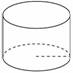
|
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

|
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

|
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
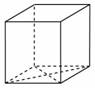
|
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

|
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

|
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2. , а высота равна 2.

|
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2. , а высота равна 2.

|
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

|
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

|
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
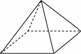
|
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

|
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

|
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?

|
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

|
Объем параллелепипеда  равен 9. Найдите объем треугольной пирамиды равен 9. Найдите объем треугольной пирамиды  . .

|
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

|
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.

|
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.

|
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.

|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

|
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

|
Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

|
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.

|
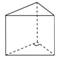
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
|
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны  . .

|
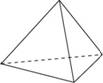
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
|
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

|
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна  . .

|
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  . .

|
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?

|
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

|
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30  . В ответе укажите . В ответе укажите  . .

|
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?

|
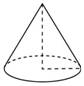
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
|
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

|
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

|
Диагональ куба равна  . Найдите его объем. . Найдите его объем.

|
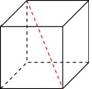
Объем куба равен  . Найдите его диагональ. . Найдите его диагональ.
|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.

|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.

|
Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
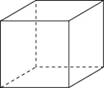
|
Диагональ прямоугольного параллелепипеда равна  и образует углы 30 и образует углы 30  , 30 , 30  и 45 и 45  с плоскостями граней параллелепипеда. Найдите объем параллелепипеда. с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

|
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60  . Одно из ребер параллелепипеда составляет с этой гранью угол в 60 . Одно из ребер параллелепипеда составляет с этой гранью угол в 60  и равно 2. Найдите объем параллелепипеда. и равно 2. Найдите объем параллелепипеда.

|
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

|
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

|
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

|
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны  и наклонены к плоскости основания под углом 30 и наклонены к плоскости основания под углом 30  . .

|
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

|
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60  . Высота пирамиды равна 6. Найдите объем пирамиды. . Высота пирамиды равна 6. Найдите объем пирамиды.

|
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

|
| От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. |
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

|
Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
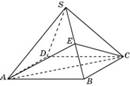
|
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

|
| Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. |
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

|
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
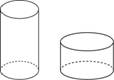
|
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на  . .

|
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на  . .

|
Конус получается при вращении равнобедренного прямоугольного треугольника  вокруг катета, равного 6. Найдите его объем, деленный на вокруг катета, равного 6. Найдите его объем, деленный на  . .

|
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  . .

|
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

|
| Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов. |
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на  . .

|
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на описан шар. Найдите объем этого шара, деленный на  . .

|
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.

|
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?

|
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?

|
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

|
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

|
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

|
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

|
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?

|
Диагональ куба равна 1. Найдите площадь его поверхности.

|
Площадь поверхности куба равна 24. Найдите его объем.

|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.

|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

|
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

|
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

|
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

|
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

|
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

|
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

|
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

|
Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на  . .

|
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

|
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
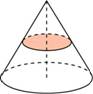
|
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

|
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

|
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  . .

|
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

|
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2. , а высота равна 2.
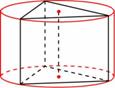
|
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.

|
| Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза? |
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на  . .

|
Объем шара равен 288  . Найдите площадь его поверхности, деленную на . Найдите площадь его поверхности, деленную на  . .

|
Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

|
Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.

|
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

|
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.

|
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

|
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45  . Найдите объем пирамиды. . Найдите объем пирамиды.

|
Объем параллелепипеда  равен 12. Найдите объем треугольной пирамиды равен 12. Найдите объем треугольной пирамиды  . .

|
Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

|
Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
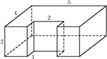
|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите  . .
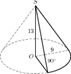
|
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите  . .

|
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите  . .

|
Вершина A куба  со стороной со стороной  является центром сферы, проходящей через точку является центром сферы, проходящей через точку  . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину  . .
|
Середина ребра куба со стороной  является центром шара радиуса является центром шара радиуса  . Найдите площадь . Найдите площадь  части поверхности шара, лежащей внутри куба. В ответе запишите части поверхности шара, лежащей внутри куба. В ответе запишите  . .
|
Объем параллелепипеда  равен равен  . Найдите объем треугольной пирамиды . Найдите объем треугольной пирамиды  . .

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Объем тетраэдра равен  Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

|
Площадь поверхности тетраэдра равна  . Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра. . Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.

|
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
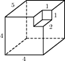
|
Найдите объем параллелепипеда  , если объем треугольной пирамиды , если объем треугольной пирамиды  равен 3. равен 3.

| ||
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

| ||
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

| ||
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  , ,  прямоугольного параллелепипеда прямоугольного параллелепипеда  , у которого , у которого  , ,  , , 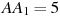 . .
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  прямоугольного параллелепипеда прямоугольного параллелепипеда  , у которого , у которого  , ,  , , 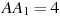 . .
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  прямоугольного параллелепипеда прямоугольного параллелепипеда  , у которого , у которого  , ,  , , 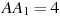 . .
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  прямоугольного параллелепипеда прямоугольного параллелепипеда  , у которого , у которого  , ,  , , 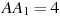 . .
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  прямоугольного параллелепипеда прямоугольного параллелепипеда  , у которого , у которого  , ,  , , 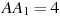 . .
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  правильной треугольной призмы правильной треугольной призмы 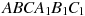 , площадь основания которой равна 2, а боковое ребро равно 3. , площадь основания которой равна 2, а боковое ребро равно 3.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  правильной треугольной призмы правильной треугольной призмы 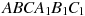 , площадь основания которой равна 3, а боковое ребро равно 2. , площадь основания которой равна 3, а боковое ребро равно 2.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  правильной треугольной призмы правильной треугольной призмы 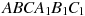 , площадь основания которой равна 4, а боковое ребро равно 3. , площадь основания которой равна 4, а боковое ребро равно 3.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3. , площадь основания которой равна 4, а боковое ребро равно 3.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 3. , площадь основания которой равна 6, а боковое ребро равно 3.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  , ,  , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 2. , площадь основания которой равна 6, а боковое ребро равно 2.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  , ,  , ,  , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 2. , площадь основания которой равна 6, а боковое ребро равно 2.
|
Найдите объем многогранника, вершинами которого являются точки  , ,  , ,  , ,  правильной шестиугольной призмы правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 3. , площадь основания которой равна 6, а боковое ребро равно 3.
|
| Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара. |
| Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра. |
| Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем цилиндра. |
| Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса. |
| Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара. |
Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

|
| Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра. |
Куб вписан в шар радиуса  . Найдите объем куба. . Найдите объем куба.
|
| Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза? |
| Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра. |
Куб вписан в шар радиуса  . Найдите объем куба. . Найдите объем куба.
|
| Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза? |
Найдите объем правильной шестиугольной призмы, все ребра которой равны  . .
|
| Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра. |
| <== предыдущая лекция | | | следующая лекция ==> |
| Мощно выводит продукты распада, бактерии, вирусы, токсины (детоксикацонное действие т.е. вывод без обезвоживания организма) | | | Сорок метров или двадцать кило |
Не нашли, что искали? Воспользуйтесь поиском: