
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Момент импульса и момент силы. Динамика вращения твёрдого тела
 Скорости точки А соответствует импульс частицы тела в этой точке
Скорости точки А соответствует импульс частицы тела в этой точке  . (Рис.2)
. (Рис.2)
Рис.2
Рассмотрим плоскость, содержащую этот импульс и радиус-вектор 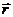 точки А относительно точки О оси вращения. (Рис.3)
точки А относительно точки О оси вращения. (Рис.3)
 Моментом импульса называется вектор
Моментом импульса называется вектор 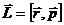 . Он перпендикулярен рассматриваемой плоскости и направлен вдоль оси вращения, как и векторы
. Он перпендикулярен рассматриваемой плоскости и направлен вдоль оси вращения, как и векторы  и
и  .
.
Модуль  , где величина
, где величина  плечо вектора
плечо вектора  относительно точки О.
относительно точки О.
 .
.
 угол между векторами
угол между векторами 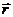 и
и  .
.
Рис.3
Момент импульса изменяется, только если на частицу действует вращающая сила. Если она приложена к объекту не в центре масс, то она создаёт вращающий момент 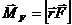 (момент силы), или в скалярной форме МF = rFsinα, где α – угол между вектором силы и радиус-вектором вращающейся точки относительно оси вращения.
(момент силы), или в скалярной форме МF = rFsinα, где α – угол между вектором силы и радиус-вектором вращающейся точки относительно оси вращения.
(Рис.4, аналогичен рис.3).
Рис.4
b = r sinα – плечо силы, т.е. кратчайшее расстояние от оси вращения объекта до направления действия силы. Можно записать в скалярной форме 
 .
.
Момент импульса и момент силы связаны с моментом инерции тела: если ось вращения неподвижна, то в проекции на неё момент силы 
и момент импульса  , где
, где 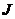 – момент инерции объекта.
– момент инерции объекта.
Момент инерции тела определяется как  , т.е. выделяется малый участок тела массой
, т.е. выделяется малый участок тела массой 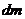 , определяется расстояние
, определяется расстояние  от него до оси вращения и берётся интеграл по всему телу.
от него до оси вращения и берётся интеграл по всему телу.
Момент инерции определяет инерционные свойства тела при его вращении (как масса при поступательном движении).
Момент инерции материальной точки относительно оси вращения 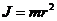 .
.
Для некоторых симметричных однородных тел момент инерции относительно геометрической оси вращения приводится обычно в таблице:
- тонкостенный цилиндр, кольцо, обруч радиуса  -
- 
- сплошной цилиндр, диск радиуса  -
- 
- шар радиуса  -
- 
- тонкий стержень длины 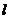 :
:
а) ось проходит через центр масс стержня перпендикулярно ему - 
б) ось проходит через конец стержня перпендикулярно ему - 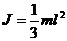
- тонкое кольцо, если ось вращения лежит в плоскости кольца и проходит через его центр -  .
.
Теорема Штейнера
Момент инерции тела 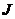 относительно произвольной оси вращения равен моменту инерции
относительно произвольной оси вращения равен моменту инерции  относительно оси, параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния
относительно оси, параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния  между осями.:
между осями.:

Теорема Штейнера позволяет определить момент инерции тела относительно любой оси вращения.
В каждой конкретной задаче для твёрдого тела нужно найти вращающие силы, сложить алгебраически их моменты и записать основное уравнение динамики:  .
.
Если его недостаточно для ответа на вопрос задачи, нужно записать ещё и второй закон Ньютона для всех действующих на объект сил.
Задача 1
На горизонтальную неподвижную ось насажен блок в виде сплошного цилиндра массы 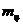 . Через него перекинута невесомая верёвка, на концах которой висят два человека массой
. Через него перекинута невесомая верёвка, на концах которой висят два человека массой  каждый. Один человек начинает подниматься с ускорением
каждый. Один человек начинает подниматься с ускорением  относительно верёвки. С каким ускорением относительно неподвижной системы координат станет двигаться другой человек? (Рис.5)
относительно верёвки. С каким ускорением относительно неподвижной системы координат станет двигаться другой человек? (Рис.5)
Дано: mц , mо ,  .
.  -?
-?
 Рис.5
Рис.5
Как только один человек начинает подниматься по верёвке, вся система приходит в движение: движется по блоку верёвка, заставляя его поворачиваться вокруг оси; висящий на верёвке другой человек тоже вместе с ней начинает перемещаться относительно комнаты.
Ускорение требуется найти для второго человека, для него уравнение движения (он относительно верёвки неподвижен):

Неизвестна сила натяжения его части верёвки 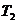 . Поскольку блок вращается, значит, силы
. Поскольку блок вращается, значит, силы  и
и 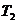 не равны. Сила
не равны. Сила 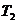 входит ещё в основное уравнение динамики для блока. Для него вращающими силами являются силы натяжения обеих сторон верёвки. Плечом для этих сил является радиус блока.
входит ещё в основное уравнение динамики для блока. Для него вращающими силами являются силы натяжения обеих сторон верёвки. Плечом для этих сил является радиус блока. 
Сила  входит в уравнение Ньютона для первого человека:
входит в уравнение Ньютона для первого человека:
 , так как он движется и относительно верёвки и вместе с верёвкой тоже.
, так как он движется и относительно верёвки и вместе с верёвкой тоже.
Итак, есть система трёх уравнений:
 ;
;  ;
; 
Момент инерции блока  . Угловое ускорение
. Угловое ускорение  ,
,
а тангенциальное ускорение точек обода блока равно линейному ускорению любой точки верёвки, а значит, и второго человека:  , поэтому
, поэтому
 =
=  и
и 
Из двух первых уравнений 
Приравняем оба уравнения для сил натяжения:
 , откуда получаем
, откуда получаем 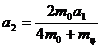
(разобрали, должны решить сами)
Не нашли, что искали? Воспользуйтесь поиском: