
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Проекции кривых линий
Кривые линии могут быть плоскими и пространственными. Они могут быть заданы аналитически с помощью уравнений и графически с помощью чертежа. В начертательной геометрии кривые линии задают с помощью чертежа.
Для построения проекций кривых линий необходимо знать приемы построения некоторых локальных характеристик: радиуса и центра кривизны, касательной, нормали и др.
2.3.1. Плоские кривые линии. Плоскими называются кривые линии, все точки которых принадлежат одной единственной плоскости. Искривленность кривой характеризуется радиусом кривизны или кривизной.
 Окружность, соприкасающаяся с кривой а в данной точке M (рис. 2.29) проходит через точку M и бесконечно близкие от нее точки M1 и M2. Радиус этой окружности называется радиусом кривизны, а центр ее - центром кривизны. Кривизной (К) называется величина, обратная радиусу, т. е. K= 1/ R.
Окружность, соприкасающаяся с кривой а в данной точке M (рис. 2.29) проходит через точку M и бесконечно близкие от нее точки M1 и M2. Радиус этой окружности называется радиусом кривизны, а центр ее - центром кривизны. Кривизной (К) называется величина, обратная радиусу, т. е. K= 1/ R.
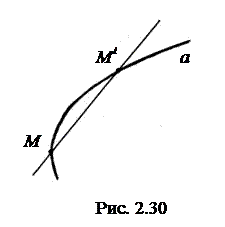 Касательной в данной точке M к кривой a (рис. 2.30) называется предельное положение секущей прямой, проведенной через точку M, когда ее длина становится равной нулю. На рис. 2.30 проведена секущая
Касательной в данной точке M к кривой a (рис. 2.30) называется предельное положение секущей прямой, проведенной через точку M, когда ее длина становится равной нулю. На рис. 2.30 проведена секущая
MM1. Пусть точка M1 двигается вдоль кривой по направлению к точке M. В момент совпадения точек M1 и M секущая
становится касательной.
Нормалью в данной точке M называется прямая, перпендикулярная к касательной.
Центр кривизны (центр соприкасающейся окружности) всегда лежит на нормали. Касательная как с плоской, так и с пространственной кривой имеет одну точку соприкосновения. Следовательно, проекция касательной к пространственной кривой будет касательной к проекции кривой, так как будет иметь с проекцией кривой только одну точку соприкосновения.
Рассмотрим практические способы построения касательных к плоским изображениям кривых, которые также могут быть проекциями пространственных кривых.
Построение касательной с помощью зеркальца. К изображению кривой в данной точке ребром приставляют зеркальце. Ставят его поперек кривой и поворачивают его до тех пор, когда отражение кривой и сама кривая будут представлять собой плавную, без изломов линию. В этот момент ребро зеркальца направлено точно по нормали. Касательная будет к ней перпендикулярна.
Построение касательной с помощью кривой ошибок. Кривой ошибок называется кривая линия, каждая точка которой строится по некоторому правилу. Только одна точка кривой ошибок отвечает необходимому условию. Все остальные точки являются ошибками.
 Пусть, например, через точку K требуется провести касательную t к кривой l (рис.2.31). Для этого выполняем следующие действия:
Пусть, например, через точку K требуется провести касательную t к кривой l (рис.2.31). Для этого выполняем следующие действия:
1) Через точку K проводим несколько секущих AB (A1B1, A2B2 и A3B3) и каждую делим пополам, обозначив середины секущих буквой C (C1, C2 и C3).
2) Соединяем точки C1, C2 и C3 плавной кривой и получаем кривую ошибок m. Продолжаем m до пересечения с заданной кривой l в точке M. В точке касания длина секущей равна нулю и ее середина совпадает с точкой касания. Поэтому считаем, что точка M пересечения кривой ошибок m с заданной кривой l и есть точка касания.
3) Точку K соединяем с M и получаем касательную t.
Пусть через точку M кривой l необходимо построить касательную t и нормаль n (рис. 2.32).
Последовательность построений в этом случае будет следующая:
1) В произвольном месте чертежа проводим прямую i примерно перпендикулярно будущей касательной.
2) Через точку M проводим ряд секущих a, b, c с одной и d, e, f с другой стороны от точки M, продолжая их до пересечения с прямой i.
3) От точек A, B, C пересечения секущих a, b, c с прямой i вдоль их откладываем длины секущих MA1, MB1, и MC1 слева от прямой i и получаем точки A2, B2 и C2. Для секущих d, e, f длины MD1, ME1 и MF1 откладываем справа от прямой i и получаем точки D2, E2 и F2.
4) Точки A2, B2, C2, …, F2 соединяем плавной кривой и получаем кривую ошибок m, которая пересекается с прямой i в точке K.
5) Соединяем точку M с точкой K прямой t, которая является секущей нулевой длины, т. е. касательной к заданной кривой l в точке M.
6) Через точку M перпендикулярно касательной t проводим нормаль n.
 |
|
|
|

 |
2.3.2. Пространственные кривые линии. Пространственные кривые линии имеют двоякую кривизну. Все точки пространственной кривой не лежат в одной плоскости. Ознакомимся, в качестве примера, с цилиндрической винтовой линией, которая имеет большое применение в технике.
Цилиндрическая винтовая линия располагается на поверхности прямого кругового цилиндра. Она образуется при сложном движении точки. Точка движется равномерно и прямолинейно вдоль образующей цилиндра и равномерно вращается вместе с образующей вокруг оси цилиндра.
Винтовая линия называется правой, если при своем поступательном движении от наблюдателя точка вращается по ходу часовой стрелки, и левой, если против хода часовой стрелки. Построение проекций цилиндрической винтовой линии дано на рис. 2.33.
Пусть имеется цилиндр диаметром d, с осью i. Наметим 12 образующих цилиндра, расположенных на равных расстояниях от друг друга. Будем считать, что образующая, переходя из одного положения в другое, равномерно вращается вокруг оси i. Вверх вдоль образующей движется точка. При повороте образующей на 1/12 оборота точка перемещается вверх на 1/12 шага h. Шагом винтовой линии называется величина перемещения точки параллельно оси при ее повороте на один полный оборот.
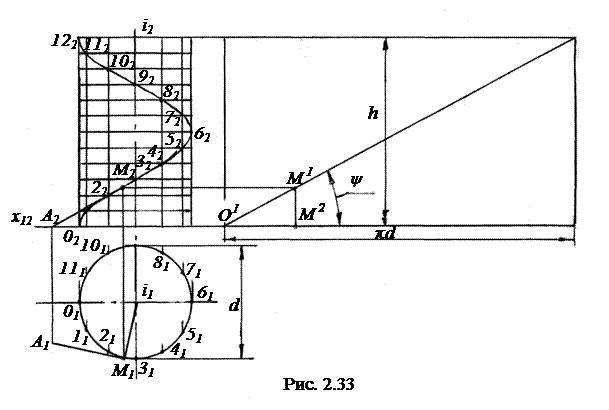

Соединяя последовательно фронтальные проекции полученных точек, строим фронтальную проекцию винтовой линии, которая представляет собой синусоиду.
Горизонтальной проекцией винтовой линии является окружность. Если развернуть цилиндрическую поверхность вместе с нанесенной на нее винтовой линией, то вращательное движение образующей на развертке превращается в ее поступательное движение вдоль развернутой окружности основания цилиндра.
В результате сложения двух равномерных поступательных движений вдоль развернутой окружности вправо и вдоль образующей вверх образуется прямая линия. Угол наклона развернутой винтовой линии к основанию:
Ψ= arctg  ,
,
где h - шаг винтовой линии; d - диаметр образующего цилиндра.
Угол Ψ называется углом наклона винтовой линии. Если навернуть винтовую линию обратно на цилиндр, то касательные в каждой точке винтовой линии наклонены к плоскости основания цилиндра под постоянным углом Ψ.
Построим касательную к винтовой линии в точке M. Как было показано выше, проекция касательной к кривой линии касательна к проекции этой кривой.
Возьмем некоторую точку M, принадлежащую винтовой линии и заданной проекциями M1 и M2, и проведем через нее касательную к винтовой линии.
Горизонтальная проекция касательной к винтовой линии будет касательна к окружности, в которую она проецируется на П1, и перпендикулярна радиусу i1M1. При построении касательной к фронтальной проекции винтовой линии используем свойство одинакового наклона всех касательных.
Отметим на развертке винтовой линии точку M1, соответствующую пространственной точке M, лежащей на винтовой линии. Из M1 опускаем перпендикуляр к развернутому основанию цилиндра и получаем точку M2. При этом отрезок основания O1M2 равен дуге окружности, на которую опирается часть винтовой линии от ее начала до точки M. Отрезок O1M2 называется подкасательной.
Из горизонтальной проекции M1 проводим касательную к окружности и откладываем на ней отрезок, равный подкасательной O1M2, и получим точку A1 - основание касательной. Точка A1 лежит на плоскости П1, т. к. A 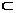 П1. Фронтальная проекция A2 этой точки лежит на оси x12. Фронтальная проекция касательной проходит через проекции A2 и M2.
П1. Фронтальная проекция A2 этой точки лежит на оси x12. Фронтальная проекция касательной проходит через проекции A2 и M2.
Можно представить себе винтовую линию и на других поверхностях, например на конической поверхности, на сфере и т. д. Если вращать образующую конической поверхности и перемещать вдоль нее точку, то образуется коническая винтовая линия. Если вращать окружность вокруг своей оси и вдоль нее перемещать точку, то образуется сферическая винтовая линия.
Не нашли, что искали? Воспользуйтесь поиском: