Вертикальные углы равны.

3. Признаки равенства треугольников.

- по двум сторонам и углу между ними;

- по стороне и двум прилегающим к ней углам;

- по трем сторонам.

4. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой треугольника называют отрезок прямой, заключенной между вершиной и точкой ее пересечения с противоположной стороной, которая делит угол пополам.

Высота треугольника – это отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону, или на ее продолжение.

5.Треугольник называют равнобедренным, если у него две стороны равны.

- в равнобедренном треугольнике углы при основании равны;

- если в треугольнике два угла равны, то он равнобедренный;

- в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

6. Треугольник называется прямоугольным, если у него есть прямой угол. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой. Остальные две стороны, называются катетами.

Свойства сторон и углов прямоугольного треугольника:

- углы, противолежащие катетам – острые;

- гипотенуза больше любого из катетов;

- катет, лежащий против угла в 30 , равен половине гипотенузы.

Признаки равенства прямоугольных треугольников:

- по катету и острому углу;

- по двум катетам;

- по гипотенузе и катету;

- по гипотенузе и острому углую

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

7. В треугольнике против большей стороны лежит больший угол, против большего угла лежит большая сторона.

8. (Неравенство треугольника). У каждого треугольника сумма двух сторон больше третьей стороны.

9. Внешним углом треугольника называется угол, смежный внутреннему углу треугольника.

10. Сумма внутренних углов треугольника:

- сумма углов треугольника равна 180^°;

- внешний угол треугольника равен сумме двух других углов, не смежных с ним.

- сумма острых углов прямоугольного треугольника равна 90^°.

11. Отрезок, соединяющий середины боковых сторон треугольника называется средней линией треугольника.

Средняя линия треугольника обладает свойством – она параллельна основанию треугольника и равна ее половине.

12.Свойства серединного перпендикуляра отрезка:

- точка лежащая на серединном перпендикуляре одинаково удалена от концов отрезка;

- любая точка, одинаково удаленная от концов отрезка, лежит на серединном перпендикуляре.

Свойства биссектрисы угла:

- любая точка, лежащая на биссектрисе угла, одинаково удалена от сторон угла;

- любая точка, одинаково удаленная от сторон угла, лежит на биссектрисе угла.

13. Существование окружности, описанной около треугольника:

- все три серединные перпендикуляры треугольника пересекаются в одной точке и эта точка является центром описанной окружности. Описанная около треугольника окружность всегда существует и она единственна;

- центром описанной окружности прямоугольного треугольника является середина гипотенузы.

14. Существование вписанной в треугольник окружности:

- все три биссектрисы треугольника пересекаются в одной точке и эта точка является центром вписанной окружности.

-вписанная в треугольник окружность всегда существует и она единственна.

15. Признаки параллельности прямых.

Теоремы о параллельности и перпендикулярности прямых:

- две прямые, параллельные третьей - параллельны;

- если при пересечении двух прямых третьей, накрест лежащие углы равны, односторонние углы в сумме равны 180^°, соответственные углы равны, то эти прямые параллельны;

- если параллельные прямые пересечены третьей прямой, то накрест лежащие углы, односторонние углы в сумме равны 180^°, соответственные углы равны.

- две прямые, перпендикулярные одной и той же прямой – параллельны;

- прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и второй.

16. Окружность – множество всех точек плоскости, равноудаленных от одной точки.

Хорда – отрезок, соединяющий две точки окружности.

Диаметр – хорда, проходящая через центр.

Касательная – прямая, имеющая с окружностью одну общую точку.

Центральный угол – угол с вершиной в центре окружности.

Вписанный угол – угол с вершиной на окружности, стороны которого пересекают окружность.

Теоремы, относящиеся к окружности:

- радиус, проведенный в точку касания, перпендикулярен касательной;

- диаметр, проходящий через середину хорды, перпендикулярен ей;

- квадрат длины касательной равен произведению длины секущей на ее внешнюю часть;

- центральный угол измеряется градусной мерой дуги, на которую он опирается;

- вписанный угол измеряется половиной дуги, на которую он опирается;

- касательные, проведенные к окружности из одной точки, равны;

17. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Признаки параллелограмма. Свойства параллелограмма:

- противоположные стороны равны;

- противоположные углы равны;

- диагонали параллелограмма делятся точкой пересечения пополам;

- если в выпуклом четырехугольнике противоположные стороны равны, то такой четырехугольник – параллелограмм;

- если в выпуклом четырехугольнике две стороны равны и параллельны, то такой четырехугольник – параллелограмм;

- если в выпуклом четырехугольнике диагонали делятся точкой пересечения пополам, то такой четырехугольник – параллелограмм;

18. Параллелограмм, все стороны которого равны, называется ромбом.

Теорема Фалеса.

Если параллельные прямые, пересекающие стороны угла, отсекают на одной стороне равные отрезки, то эти прямые отсекают на другой стороне также равные отрезки.

Теорема Пифагора.

В прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов: .

26. Теорема косинусов.

В любом треугольнике, квадрат стороны равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними: .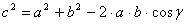

Теорема синусов.

Стороны треугольника пропорциональны синусам противоположных углов: , где - радиус окружности, описанной около этого треугольника.

28. Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.

29. Три прямые, содержащие высоты треугольника, пересекаются в одной точке.

30. Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим его сторонам.

31. Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180^°.

32. Четырехугольник можно описать вокруг окружности, если суммы длин противоположных сторон равны.

Не нашли, что искали? Воспользуйтесь поиском: